Posts filed under ‘Network thoughts’
The added benefit of network data: Assessing impact of suppliers and buyers on CDS spreads
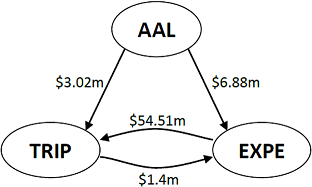 Networks has the potential to increase the explanatory power of models. The content of this post, and accompanying paper, quantifies the size of this effect for predicting the financial health of companies. It is my hope that it can help drive more research into networks and enable more organizations to develop better models and understand interdependencies to a greater extent.
Networks has the potential to increase the explanatory power of models. The content of this post, and accompanying paper, quantifies the size of this effect for predicting the financial health of companies. It is my hope that it can help drive more research into networks and enable more organizations to develop better models and understand interdependencies to a greater extent.
Companies do not operate in a vacuum. As companies move towards an increasingly specialized production function and their reach is becoming truly global, their aptitude in managing and shaping their inter-organizational network is a determining factor in measuring their health. Current models of company financial health often lack variables explaining the inter-organizational network, and as such, assume that (1) all networks are the same and (2) the performance of partners do not impact companies. This paper aims to be a first step in the direction of removing these assumptions. Specifically, the impact is illustrated by examining the effects of customer and supplier concentrations and partners’ credit risk on credit-default swap (CDS) spreads while controlling for credit risk and size. We rely upon supply-chain data from Bloomberg that provides insight into companies’ relationships. The empirical results show that a well diversified customer network lowers CDS spread, while having stable partners with low default probabilities increase spreads. The latter result suggests that successful companies do not focus on building a stable eco-system around themselves, but instead focus on their own profit maximization at the cost of the financial health of their suppliers’ and customers’. At a more general level, the results indicate the importance of considering the inter-organizational networks, and highlight the value of including network variables in credit risk models.
Continue Reading February 23, 2016 at 1:20 am Leave a comment
Why Anchorage is not (that) important: Binary ties and Sample selection
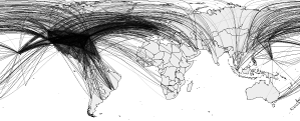 A surprising finding when analysing airport networks is the importance of Anchorage airport in Alaska. In fact, it is the most central airport in the network when applying betweenness! I do not believe this finding is completely accurate due to two reasons: (1) there is a potential for measurement error when not including tie weights (i.e., assigning the same importance to the connection between London Heathrow and New York’s JFK as to the connection between Pack Creek Airport and Sitka Harbor Sea Plane Base in Alaska), and (2) relying on US data only leads to sample selection as the airport network is a global system. This post highlights how to use a weighted betweenness measure as well as the extent of the sample selection issue.
A surprising finding when analysing airport networks is the importance of Anchorage airport in Alaska. In fact, it is the most central airport in the network when applying betweenness! I do not believe this finding is completely accurate due to two reasons: (1) there is a potential for measurement error when not including tie weights (i.e., assigning the same importance to the connection between London Heathrow and New York’s JFK as to the connection between Pack Creek Airport and Sitka Harbor Sea Plane Base in Alaska), and (2) relying on US data only leads to sample selection as the airport network is a global system. This post highlights how to use a weighted betweenness measure as well as the extent of the sample selection issue.
Degree Centrality and Variation in Tie Weights
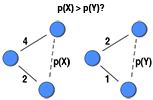
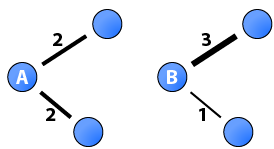 A central metric in network research is the number of ties each node has, degree. Degree has been generalised to weighted networks as the sum of tie weights (Barrat et al., 2004), and as a function of the number of ties and the sum of their weights (Opsahl et al., 2010). However, all these measures are insensitive to variation in the tie weights. As such, the two nodes in this diagram would always have the same degree score. This post showcases a new measure that uses a tuning parameter to control whether variation should be taken favourable or discount the degree centrality score of a focal node.
A central metric in network research is the number of ties each node has, degree. Degree has been generalised to weighted networks as the sum of tie weights (Barrat et al., 2004), and as a function of the number of ties and the sum of their weights (Opsahl et al., 2010). However, all these measures are insensitive to variation in the tie weights. As such, the two nodes in this diagram would always have the same degree score. This post showcases a new measure that uses a tuning parameter to control whether variation should be taken favourable or discount the degree centrality score of a focal node.
Closeness centrality in networks with disconnected components
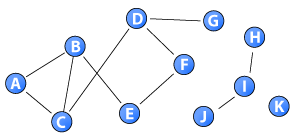 A key node centrality measure in networks is closeness centrality (Freeman, 1978; Wasserman and Faust, 1994). It is defined as the inverse of farness, which in turn, is the sum of distances to all other nodes. As the distance between nodes in disconnected components of a network is infinite, this measure cannot be applied to networks with disconnected components (Opsahl et al., 2010; Wasserman and Faust, 1994). This post highlights a possible work-around, which allows the measure to be applied to these networks and at the same time maintain the original idea behind the measure.
A key node centrality measure in networks is closeness centrality (Freeman, 1978; Wasserman and Faust, 1994). It is defined as the inverse of farness, which in turn, is the sum of distances to all other nodes. As the distance between nodes in disconnected components of a network is infinite, this measure cannot be applied to networks with disconnected components (Opsahl et al., 2010; Wasserman and Faust, 1994). This post highlights a possible work-around, which allows the measure to be applied to these networks and at the same time maintain the original idea behind the measure.
Online Social Network-dataset now available
 The Online Social Network-dataset used in my Ph.D. thesis is now available on the Dataset-page. This network has also been described in Patterns and Dynamics of Users’ Behaviour and Interaction: Network Analysis of an Online Community and used in Prominence and control: The weighted rich-club effect and Clustering in weighted networks. The network originate from an online social network among students at University of California, Irvine. The edgelist includes the users that sent or received at least one message during that period (1,899). A total number of 59,835 online messages were sent among these over 20,296 directed ties.
The Online Social Network-dataset used in my Ph.D. thesis is now available on the Dataset-page. This network has also been described in Patterns and Dynamics of Users’ Behaviour and Interaction: Network Analysis of an Online Community and used in Prominence and control: The weighted rich-club effect and Clustering in weighted networks. The network originate from an online social network among students at University of California, Irvine. The edgelist includes the users that sent or received at least one message during that period (1,899). A total number of 59,835 online messages were sent among these over 20,296 directed ties.
Similarity between node degree and node strength
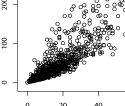 This post explores the relationship between node degree and node strength in an online social network. In the online social network, heterogeneity in nodes’ average tie weight across different levels of degree had been reported
This post explores the relationship between node degree and node strength in an online social network. In the online social network, heterogeneity in nodes’ average tie weight across different levels of degree had been reported . Although degree and average tie weight are significantly correlated, this post argues for the similarity of degree and node strength. In particular, high pair-wise correlation between degree and strength is found. In addition, power-law exponents of degree distributions and strength distribution are reported. The exponents are strikingly similar, in fact, they are almost identical.
. Although degree and average tie weight are significantly correlated, this post argues for the similarity of degree and node strength. In particular, high pair-wise correlation between degree and strength is found. In addition, power-law exponents of degree distributions and strength distribution are reported. The exponents are strikingly similar, in fact, they are almost identical.
Continue Reading October 16, 2009 at 12:57 pm Leave a comment
Projecting two-mode networks onto weighted one-mode networks
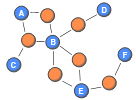 This post highlights a number of methods for projecting both binary and weighted two-mode networks (also known as affiliation or bipartite networks) onto weighted one-mode networks. Although I would prefer to analyse two-mode networks in their original form, few methods exist for that purpose. These networks can be transformed into one-mode networks by projecting them (i.e., selecting one set of nodes, and linking two nodes if they are connected to the same node of the other set). Traditionally, ties in the one-mode networks are without weights. By carefully considering multiple ways of projecting two-mode networks onto weighted one-mode networks, we can maintain some of the richness contained within the two-mode structure. This enables researchers to conduct a deeper analysis than if the two-mode structure was completely ignored.
This post highlights a number of methods for projecting both binary and weighted two-mode networks (also known as affiliation or bipartite networks) onto weighted one-mode networks. Although I would prefer to analyse two-mode networks in their original form, few methods exist for that purpose. These networks can be transformed into one-mode networks by projecting them (i.e., selecting one set of nodes, and linking two nodes if they are connected to the same node of the other set). Traditionally, ties in the one-mode networks are without weights. By carefully considering multiple ways of projecting two-mode networks onto weighted one-mode networks, we can maintain some of the richness contained within the two-mode structure. This enables researchers to conduct a deeper analysis than if the two-mode structure was completely ignored.
The importance of allowing ties to decay
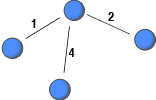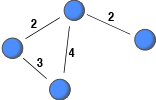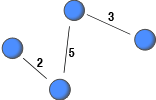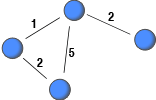 Recently, a number of network dataset have been constructed from archival data (e.g., email logs) with the aim to study human interaction. This has allowed researchers to study large-scale social networks. If the archival data does not included information about the severing or weakening of ties, non-relevant interaction among people, which occurred far in the past, might be deemed relevant. This post highlights this issue and suggests imposing a lifespan on interactions to record only relevant ties with the current strength.
Recently, a number of network dataset have been constructed from archival data (e.g., email logs) with the aim to study human interaction. This has allowed researchers to study large-scale social networks. If the archival data does not included information about the severing or weakening of ties, non-relevant interaction among people, which occurred far in the past, might be deemed relevant. This post highlights this issue and suggests imposing a lifespan on interactions to record only relevant ties with the current strength.
Betweenness in weighted networks
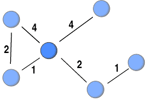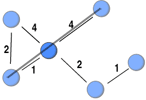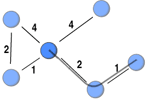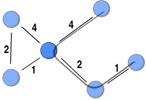 This post highlights a generalisation of Freeman’s (1978) betweenness measure to weighted networks implicitly introduced by Brandes (2001) when he developed an algorithm for calculating betweenness faster. Betweenness is a measure of the extent to which a node funnels transactions among all the other nodes in the network. By funnelling the transactions, a node can broker. This could be by taking a cut (e.g. Ukraine controls most gas pipelines from Russia to Europe) or distorting the information being transmitted to its advantage.
This post highlights a generalisation of Freeman’s (1978) betweenness measure to weighted networks implicitly introduced by Brandes (2001) when he developed an algorithm for calculating betweenness faster. Betweenness is a measure of the extent to which a node funnels transactions among all the other nodes in the network. By funnelling the transactions, a node can broker. This could be by taking a cut (e.g. Ukraine controls most gas pipelines from Russia to Europe) or distorting the information being transmitted to its advantage.
Operationalisation of tie strength in social networks
 The method used to operationalise ties’ strength into weights affects the outcomes of weighted networks measures. Simply assigning 1, 2, and 3 to three different levels of tie strength might not be appropriate as this scale might misrepresent the actually difference among the three levels (using an ordinal scale). In this post, I highlight issues with collecting weighted social network data from surveys.
The method used to operationalise ties’ strength into weights affects the outcomes of weighted networks measures. Simply assigning 1, 2, and 3 to three different levels of tie strength might not be appropriate as this scale might misrepresent the actually difference among the three levels (using an ordinal scale). In this post, I highlight issues with collecting weighted social network data from surveys.
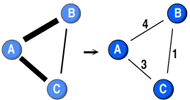
Average shortest distance in weighted networks
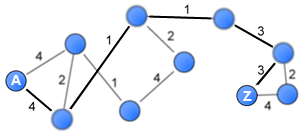 The average distance that separate nodes in a network became a famous measure following Milgram’s six-degrees of separation experiment in 1967 that found that people in the US were on average 6-steps from each other. This post proposes a generalisation of this measure to weighted networks by building on work by Dijkstra (1959) and Newman (2001).
The average distance that separate nodes in a network became a famous measure following Milgram’s six-degrees of separation experiment in 1967 that found that people in the US were on average 6-steps from each other. This post proposes a generalisation of this measure to weighted networks by building on work by Dijkstra (1959) and Newman (2001).
Local weighted rich-club measure
This post proposes a local (node-level) version of the Weighted Rich-club Effect (PRL 101, 168702). By incorporating this measure into a regression analysis, the impact of targeting efforts towards prominent nodes on performance can be studied.
Network? Weighted network?
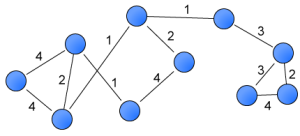 Networks are the cornerstone of this blog, therefore I have decided to make the first post my definition of a network and a few basic network measures.
Networks are the cornerstone of this blog, therefore I have decided to make the first post my definition of a network and a few basic network measures.
 RSS feed
RSS feed