Betweenness in weighted networks
February 20, 2009 at 12:00 am 6 comments
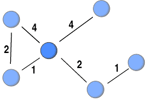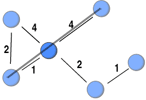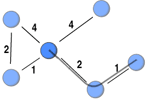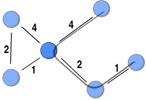This post highlights a generalisation of Freeman’s (1978) betweenness measure to weighted networks implicitly introduced by Brandes (2001) when he developed an algorithm for calculating betweenness faster. Betweenness is a measure of the extent to which a node funnels transactions among all the other nodes in the network. By funnelling the transactions, a node can broker. This could be by taking a cut (e.g. Ukraine controls most gas pipelines from Russia to Europe) or distorting the information being transmitted to its advantage.
Entry filed under: Network thoughts. Tags: betweenness, centrality, closeness, complex networks, graphs, local, network, shortest distance, shortest path, social network analysis, strength of ties, valued networks, weighted networks.
RSS feed
Tore Opsahl 
1.
John Ihrie | April 14, 2011 at 5:26 am
I noticed your R documentation for the tnet package identifies “betweenness_w Betweenness centrality in a weighted network”. Doesn’t the betweenness centrality actually normalize the values such that a node will have a BC somewhere between 0 and 1? Is there anyway to arrive at this normalized value with your package?
Thanks
2.
Tore Opsahl | April 14, 2011 at 6:09 am
John,
Normalisation of centrality measures are troublesome for two reasons for me. First, it is unclear whether the binary betweenness measure scales with n(n-1). While this is a theoretical maximum that would be observed for the central node in a star-configuration, it becomes harder for nodes to be stars as the network grows in terms of nodes since the average degree grows slower than the number of nodes. Second, dividing by a constant does not increase the variance among nodes in a network. As such, unless you compare between networks, there is no purpose to normalising the measures. Nevertheless, if you are comparing across networks, I would claim that, due to the uncertain relationship between number of nodes and centrality measures, the networks must be comparable in size. However, if they are the same size, then there is no point to normalisation.
Having said that about the binary measures, the weighted measures do not have theoretical maxima as tie weight generally are not bound by an upper limit. Thus, it is not possible to normalise them, which to be honest, might not be such a bad idea!
Best,
Tore
3.
John Ihrie | April 14, 2011 at 10:10 pm
Tore,
Thank you very much for your response. I have another question: Is it possible to analyze mixed graphs with your package?
4.
Tore Opsahl | April 19, 2011 at 8:27 pm
John,
How do you define mixed graphs? tnet currently can only analyse weighted, two-mode, and continuously observed networks.
Tore
5.
John Ihrie | April 20, 2011 at 12:31 am
By mixed I mean some of the edges are directed, while some of the edges are undirected.
Thanks
6.
Tore Opsahl | April 20, 2011 at 7:25 am
John,
I treat these networks as directed and simply create two directed ties — one in each direction — for each undirected tie. This is also how undirected networks are represented generally in tnet.
Tore