Closeness centrality in networks with disconnected components
March 20, 2010 at 1:03 pm 59 comments
A key node centrality measure in networks is closeness centrality (Freeman, 1978; Opsahl et al., 2010; Wasserman and Faust, 1994). It is defined as the inverse of farness, which in turn, is the sum of distances to all other nodes. As the distance between nodes in disconnected components of a network is infinite, this measure cannot be applied to networks with disconnected components (Opsahl et al., 2010; Wasserman and Faust, 1994). This post highlights a possible work-around, which allows the measure to be applied to these networks and at the same time maintain the original idea behind the measure.
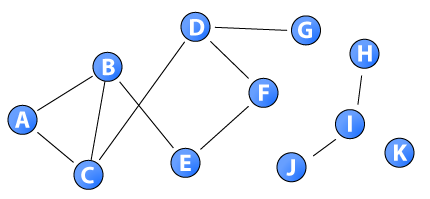This network gives a concrete example of the closeness measure. The distance between node G and node H is infinite as a direct or indirect path does not exist between them (i.e., they belong to separate components). As long as at least one node is unreachable by the others, the sum of distances to all other nodes is infinite. As a consequence, researchers have limited the closeness measure to the largest component of nodes (i.e., measured intra-component). The distance matrix for the nodes in the sample network is:
| Nodes | All inclusive | Intra-component | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | Farness | Closeness | Farness | Closeness | ||
| A | … | 1 | 1 | 2 | 2 | 3 | 3 | Inf | Inf | Inf | Inf | Inf | 0 | 12 | 0.08 | |
| B | 1 | … | 1 | 2 | 1 | 2 | 3 | Inf | Inf | Inf | Inf | Inf | 0 | 10 | 0.10 | |
| C | 1 | 1 | … | 1 | 2 | 2 | 2 | Inf | Inf | Inf | Inf | Inf | 0 | 9 | 0.11 | |
| D | 2 | 2 | 1 | … | 2 | 1 | 1 | Inf | Inf | Inf | Inf | Inf | 0 | 9 | 0.11 | |
| E | 2 | 1 | 2 | 2 | … | 1 | 3 | Inf | Inf | Inf | Inf | Inf | 0 | 11 | 0.09 | |
| F | 3 | 2 | 2 | 1 | 1 | … | 2 | Inf | Inf | Inf | Inf | Inf | 0 | 11 | 0.09 | |
| G | 3 | 3 | 2 | 1 | 3 | 2 | … | Inf | Inf | Inf | Inf | Inf | 0 | 14 | 0.07 | |
| H | Inf | Inf | Inf | Inf | Inf | Inf | Inf | … | 1 | 2 | Inf | Inf | 0 | 3 | 0.33 | |
| I | Inf | Inf | Inf | Inf | Inf | Inf | Inf | 1 | … | 1 | Inf | Inf | 0 | 2 | 0.50 | |
| J | Inf | Inf | Inf | Inf | Inf | Inf | Inf | 2 | 1 | … | Inf | Inf | 0 | 3 | 0.33 | |
| K | Inf | Inf | Inf | Inf | Inf | Inf | Inf | Inf | Inf | Inf | … | Inf | 0 | 0 | Inf | |
Although the intra-component closeness scores are not infinite for all the nodes in the network, it would be inaccurate to use them as a closeness measure. This is due to the fact that the sum of distances would contain different number of paths (e.g., there are two distance from node H to other nodes in its component, while there are six distances from node G to other nodes in its component). In fact, nodes in smaller components would generally be seen as being closer to others than nodes in larger components. Thus, researchers has focused solely on the largest component. However, this leads to a number of methodological issues, including sample selection.
To develop this measure, I went back to the original equation:
![\mbox{closeness}(i) = \sum_j \left[ d_{ij} \right]^{-1} = \frac{1}{\sum_j d_{ij}}](https://s0.wp.com/latex.php?latex=%5Cmbox%7Bcloseness%7D%28i%29+%3D+%5Csum_j+%5Cleft%5B+d_%7Bij%7D+%5Cright%5D%5E%7B-1%7D+%3D+%5Cfrac%7B1%7D%7B%5Csum_j+d_%7Bij%7D%7D&bg=ffffff&fg=414141&s=0&c=20201002)
where 
To exemplify this change, for the example network above, the inversed distances and closeness scores are:
| Nodes | Closeness | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | Sum | Normalized | ||
| A | … | 1.00 | 1.00 | 0.50 | 0.50 | 0.33 | 0.33 | 0 | 0 | 0 | 0 | 3.67 | 0.37 | |
| B | 1.00 | … | 1.00 | 0.50 | 1.00 | 0.50 | 0.33 | 0 | 0 | 0 | 0 | 4.33 | 0.43 | |
| C | 1.00 | 1.00 | … | 1.00 | 0.50 | 0.50 | 0.50 | 0 | 0 | 0 | 0 | 4.50 | 0.45 | |
| D | 0.50 | 0.50 | 1.00 | … | 0.50 | 1.00 | 1.00 | 0 | 0 | 0 | 0 | 4.50 | 0.45 | |
| E | 0.50 | 1.00 | 0.50 | 0.50 | … | 1.00 | 0.33 | 0 | 0 | 0 | 0 | 3.83 | 0.38 | |
| F | 0.33 | 0.50 | 0.50 | 1.00 | 1.00 | … | 0.50 | 0 | 0 | 0 | 0 | 3.83 | 0.38 | |
| G | 0.33 | 0.33 | 0.50 | 1.00 | 0.33 | 0.50 | … | 0 | 0 | 0 | 0 | 3.00 | 0.30 | |
| H | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 1.00 | 0.50 | 0 | 1.50 | 0.15 | |
| I | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1.00 | … | 1.00 | 0 | 2 | 0.20 | |
| J | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.50 | 1.00 | … | 0 | 1.50 | 0.15 | |
| K | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 | |
As can be seen from this table, a closeness score is attained for all nodes taking into consideration an equal number of distances for each node irrespective of the size of the nodes’ component. Moreover, nodes belonging to a larger component generally attains a higher score. This is deliberate as these nodes can reach a greater number of others than nodes in smaller components. The normalized scores are bound between 0 and 1. It is 0 if a node is an isolate, and 1 if a node is directly connected all others.
This measure can easily be extended to weighted networks by introducing Dijkstra’s (1959) algorithm as proposed in Average shortest distance in weighted networks.
References
Dijkstra, E. W., 1959. A note on two problems in connexion with graphs. Numerische Mathematik 1, 269-271.
Freeman, L. C., 1978. Centrality in social networks: Conceptual clarification. Social Networks 1, 215-239.
Opsahl, T., Agneessens, F., Skvoretz, J. (2010). Node centrality in weighted networks: Generalizing degree and shortest paths. Social Networks 32, 245-251.
Wasserman, S., Faust, K., 1994. Social Network Analysis: Methods and Applications. Cambridge University Press, New York, NY.
What to try it with your data?
Below is the code to calculate the closeness measure on the sample network above.
# Load tnet library(tnet) # Load network # Node K is assigned node id 8 instead of 10 as isolates at the end of id sequences are not recorded in edgelists net <- cbind( i=c(1,1,2,2,2,3,3,3,4,4,4,5,5,6,6,7,9,10,10,11), j=c(2,3,1,3,5,1,2,4,3,6,7,2,6,4,5,4,10,9,11,10), w=c(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1)) # Calculate measures closeness_w(net, gconly=FALSE)
Entry filed under: Network thoughts. Tags: actors, arcs, centrality, closeness, complex networks, directed networks, edges, global, graphs, hubs, Links, local, network, nodes, shortest distance, shortest path, social network analysis, strength of ties, ties, undirected networks, valued networks, vertices, weighted networks.
RSS feed
Tore Opsahl 
1.
Wolfgang Weber | September 30, 2010 at 12:48 pm
Hi Tore,
i have a question about the definition of closeness. I thought the definition is
In your example for your new solution with inversed distances and the normalized closeness you seem to use this definition in an adapted way
quasi inversed distances and re-inversed closeness, but in the first example (intra-component) its simply 1/(sum of distances).
I’m only an amateur, so please don’t be too mathematically in your answers ;-)
Wolfgang
2.
Tore Opsahl | September 30, 2010 at 3:43 pm
Wolfgang,
What you are talking about is the normalisation of closeness scores. A normalisation procedure is simply ensuring that scores are bound between 0 and 1. If you divide positive scores by its theoretical maximum, you will achieve this.
I am not a fan of normalisation as (1) it does not increase the variance among scores if you only analyse one network or networks of similar size (i.e., multiplying all scores with a constant), and (2) it is questionable whether the sum of all distances scale linearly with the number of nodes (see the small-world literature on this topic). As a result, I have not used normalised scores.
Hope this helps,
Tore
3.
Manal Rayess | January 4, 2011 at 9:30 am
Hi Tore,
tnet outputs the normailzed closeness as well, however the tutorial mentions that the output is a data.frame with two columns, node ids and closeness scores. Can you please just indicate in the tutorial that a third column (n.closeness) is output as well?
Thanks and regards.
4.
Tore Opsahl | January 4, 2011 at 9:40 am
Manal,
The third column in the normalised closeness scores (i.e., the closeness scores divided by n-1). This column is only added when gconly=FALSE. But there is no reason why it is not computed when gconly=TRUE. Will add this in the upcoming version of tnet, and change the manual. Thanks for noticing.
Best,
Tore
5.
Elizabeth Hobson | November 9, 2011 at 8:08 pm
Hi Tore,
I am comparing two networks of slightly different sizes (n=21 & n=19) and would like to normalize the closeness scores to facilitate this comparison. Since the networks are very similar in size, I don’t think I have to worry about small world scaling issues. My question has to do with the normalized closeness data. When tnet outputs closeness alpha=0, the normalized values are bounded between 0 and 1 as expected. However, if I run closeness with alpha=0.5 or 1, the normalized values exceed 1 (I get values up to 1.29). This is driven by nonnormalized closeness values that exceed n-1. For example, in one case I have n-1=20 and one node with a closeness score of 24.5 (when alpha=0.5). Does your normalization procedure only apply to closeness when using alpha=0? Could you suggest a way to normalize closeness for alpha=0.5?
Thanks for your help,
Liz
6.
Tore Opsahl | November 9, 2011 at 10:37 pm
Hi Liz,
The non-alpha=0-measures do not have a fixed maximum. As such, it is difficult to normalise the measures. Unfortunately, I do not know of a way to normalize the non-binary scores. If you find one, do let me know!
Best,
Tore
7.
sadia shah | April 19, 2011 at 9:29 am
Tore,
I am using this approach for a directed network….and i come across cases where a node X cannot be reached by another node Z because although connections between intermediate nodes (say Y) exist but not in both directions…shall i consider that the distance X and Z will be infinity?
i m waiting for a quick reply :-)
Regards,
Sadia.
8.
Tore Opsahl | April 19, 2011 at 8:25 pm
Sadia,
Great that you are fining this method interesting and applicable!
The traditional closeness measure requires all nodes to be mutally reachable. The above procedure does not have this requirement.
The distance from one node to another in a directed network might be different from the distance from the latter to the former node. The distance calculation in a directed network generally assumes that paths follow ties direction (e.g., if a has a tie with b, and b has a tie with c, the there is a path from a to c, but not from c to a). The distance_w and closeness_w-functions in tnet use this procedure.
Hope this helps,
Tore
9.
sadia shah | April 20, 2011 at 10:05 am
Thank you for noticing this comment and replying to it so quickly:)…Yes it did help…..
I need one further guidance related to the dataset i am using. it is an email network which is weighted,directed and has disconnected components…….I have some email sender nodes but their recipients are missing………
for example node X send 2 or say 3 very important emails but i do not know who were the recipients……Of course i can not deny their existance………..what could be done?
Can u suggest something?
Regards,
Sadia.
10.
Tore Opsahl | April 24, 2011 at 11:10 pm
Sadia,
An always interesting, but sometimes forgotten concept in network analysis, is the boundary of the network. Unfortunately, few, if none, network measures are able to incorporate missing nodes. Let me know how you deal with this issue.
Best,
Tore
11.
sadia shah | May 31, 2011 at 6:35 am
Tore,
I have a small issue…….while calculating the average closeness of all nodes, can i remove nodes having 0 closeness with the rest of the network by considering them to as isolated nodes? e.g. from the above network, can i remove node K while finding average?
waiting for a reply.
Sadia.
12.
Tore Opsahl | May 31, 2011 at 11:06 am
Sadia,
If you save the output from the closeness_w-function as an object called out, then you can extract the rows of out where closeness is greater than 0, and calculate the mean of the closeness column. Below is some sample code that could replace the last line in the code in the blog post.
Best,
Tore
13.
sadia shah | June 8, 2011 at 2:07 pm
tore,
thank u for the help….can u explain:
what will be the possible effect of removing “0” closeness nodes on the mean closeness of the network?
or can u recommend any other resource from where i can read or get some theoretical guidence?
ur replies always raise new questions in my mind:)
regards,
sadia.
14.
Tore Opsahl | June 9, 2011 at 11:33 am
Sadia,
By removing the nodes with a score of 0, you will increase the mean. However, this is more a question of the boundary of the analysis/network. Should isolates be included? If yes, then the 0 scores should be included. If not, then they should be removed.
Best,
Tore
15.
Chavdar Dangalchev | September 19, 2011 at 2:44 pm
Hi Tore,
How your definition is different from the definition used in:
“Latora V., Marchiori M., Efficient behavior of small-world networks,
Physical Review Letters, V. 87, p. 19, 2001.”
?
Shouldn’t you start quoting Latora and Marchiori?
Regards,
Chavdar
16.
Tore Opsahl | September 19, 2011 at 4:02 pm
Hi Chavdar,
Thank you for guiding me to this article. It is very interesting how they created a unifying small-world measure. This is something I have been thinking about for quite some time.
In this post, I focused on centrality, or more specifically, node closeness scores. You are absolutely right that the inverse of geodesic distances were also taken in Latora and Marchiori (2001); however, they did so from a different background (small-world literature) to reach a very different outcome (i.e., understanding the overall function of the network). The path of research that I was following originated with Freeman’s (1978) work on centrality. In fact, it is worth noting that the terms closeness and centrality are not even mentioned in Latora and Marchiori (2001).
The proposed measure by Latora and Marchiori (2001) enables an assessment of the connectedness of a network. Although I don’t think that the normalisation using n*(n-1) is appropriate as the small-world literature has told us that geodesic distance does not scale with n-squared, it does show how a measure to test for the existence of a backbone in networks could be created. In fact, it is exactly this where I believe the paper is contributing to the literature.
Thanks again for pointing me to this paper!
Tore
17.
Seongkyun Kim | February 18, 2012 at 8:57 pm
Hi, Tore
If I want to calculate the closeness centrality of graph centrality (Freeman, 1978, p228, p231) using your closeness method, Is it okay to use following eq?
Cc = sum of your normalized Cc (3rd c) * (2n – 3)/(n^2-3n+2)
I used whole nodes (i.e, n =11, Cc = 0.3554 suggested example matrix in this post)
Is it better to suggest the mean of the normalized closeness centrality than CC of Freem?
Thanks and regards.
18.
Seongkyun Kim | February 19, 2012 at 12:52 pm
One more Question,
I think that
normalized closeness of a node i = efficiency of a node i
mean values of all normalized closeness = Glabal Efficiency
isn’t it?
19.
Marwa | April 26, 2012 at 11:13 am
Hi, Tore,
do u have any idea please how to calculate closeness centrality using SAS ??
thanks and regards.
20.
Tore Opsahl | April 26, 2012 at 1:38 pm
Hi Marwa,
I don’t I’m afraid as my work is mainly centered on using R.
Best,
Tore
21.
peyina | July 20, 2012 at 10:21 pm
Hi Tore,
In R’s {sna} package, closeness centrality offers the formula you suggest–of obtaining the inverse of distance to other nodes before summing them. They attribute this formula to
Gil and Schmidt (1996). see http://www.inside-r.org/packages/cran/sna/docs/closeness
Thought you might like to know.
cheers, and thanks for keeping this useful blog.
P
22.
Tore Opsahl | July 23, 2012 at 3:10 pm
Hi Peyina,
Thanks for this reference! There are many implementations of similar work-arounds for this issue. I am unable to get a hold of Gil and Schmidt’s Sunbelt presentation from 1996, but it does not seem to be proposed in Gil, Schmidt, Castro, and Ruiz paper in Connections in 1997 with a similar title as they do not deal specifically with disconnected networks. Glad to attribute them here.
Tore
23.
peyina | July 23, 2012 at 4:51 pm
Right. I can’t access the 1996 conference paper either; just based my comment on the R {sna} package documentation… searched for Gil and Schmidt closeness centrality and came upon Sinclair’s article: http://www.sciencedirect.com/science/article/pii/S0378873306000116 –not sure if you have access to it). He describes G & Sch’s power centrality index as “comparable with the closeness centrality index in that it uses distances from the indexed vertex to other vertices in the calculation” ( p. 81-82)
So, hard to tell whether perhaps in their presentation, G & Sch more explicitly made a connection between their index and closeness centrality, or whether the R sna alternative for closeness was inspired by G & Sch.
cheers,
Peyina
24.
Tyler Creech | August 18, 2012 at 12:55 am
Hi Tore,
I have a question about the closeness_w function. I am trying to use this function to assess the relative influence of edges in a weighted, disconnected network, by removing one edge at a time and calculating the mean weighted closeness across all network nodes. Presumably, the edges whose removal results in the largest decrease in mean closeness are the most influential.
I have found that there are a couple edges in my network whose deletion actually causes a slight increase in the mean weighted closeness (without any changes to nodes). Do you know how this could be possible? I am using the gconly=FALSE option and alpha=1 for Dijkstra’s algorithm. I can’t see how removing any edge could increase closeness – at worst, it seems like it would have no impact, if the deleted edge wasn’t part of any shortest paths. Is this perhaps some sort of scaling issue? It makes no difference whether I use the normalized values (i.e., divided by N-1) or not, but maybe there is some additional standardization within the function that I’m not aware of?
Thanks for your help, and for developing a great R package and website. I have found both to be tremendously helpful.
Tyler
25.
Tore Opsahl | August 20, 2012 at 1:37 pm
Hi Tyler,
Great that you are finding tnet useful!
I have a suspicion that this might be due to changing network size (i.e., isolates at the end of the node id sequence are removed as the network is stored as an edgelist). If you email me the code and data, I will have a look.
Best,
Tore
26.
Tyler Creech | August 20, 2012 at 6:38 pm
Hi Tore, data and code are attached. Thanks for taking a look.
Tyler
27.
Rafael Cipullo | August 30, 2012 at 12:00 pm
Hi Tore,
Great work…
I had a problem with your tool when I tried to use on my network (n=88.000). It simply doesn’t work and appears a message “out of memory”.
Can you suggest something?
Thanks for your help,
Rafael
28.
Tore Opsahl | August 30, 2012 at 1:51 pm
Hi Rafael,
This is a problem with R. It consumes a lot of memory. Have a look at this post for running R on Amazon’s EC2 cloud: https://toreopsahl.com/2011/10/17/securely-using-r-and-rstudio-on-amazons-ec2/
If you are running the clustering coefficient calculations for one- or two-mode networks, email me as c++ versions of these metrics exists.
Best,
Tore
29.
Rafael Cipullo | August 30, 2012 at 2:20 pm
Tore,
I have another question, when I set gconly = TRUE the identification of nodes are not the same of the network. I think they are sequential in the output.
Is there an option to recover the id information of the nodes?
Thanks again
Rafael
30.
Tore Opsahl | August 30, 2012 at 2:38 pm
Rafael,
This shouldn’t be the case. As you can see from the example, node 8 is missing in the edgelist, and gets a closeness score of 0 in the output when gconly is set to TRUE. Using the closeness-function requires an N by N distance matrix to be calculated. This will be a memory issue when you have 88,000 nodes…
Best,
Tore
31.
Janet | October 2, 2012 at 12:45 am
Hi Tore,
Thank you for the program. I’m just wondering if it’s possible to input the data with each node as a 5 digit identifier, instead a number starting from 1.
I have a dataset where the nodes are identified by firm permno, which is a 5 digit number. And every time I run it, R crashes.
Thanks a lot!
Janet
32.
Tore Opsahl | October 2, 2012 at 2:20 pm
Hi Janet,
Glad you are using tnet. It is possible to use a five-digit identifier; however, this will create much larger output objects. You might want to run the compress_ids-function first on the data. If this doesn’t help, please email me the code and data that you are using, and I will have a look.
Best,
Tore
33.
Janet | November 8, 2012 at 2:59 pm
Hi Tore,
Thanks for your reply last time! I solved the problem by building an index before inputting the network.
However, I have an important question to ask you. I rerun my code and got different closeness measure as I got before. Actually, I don’t even get the right result for your example on this webpage! The code is:
net closeness_w
function (net, directed = NULL, gconly = TRUE, precomp.dist = NULL,
alpha = 1)
{
if (is.null(attributes(net)$tnet))
net <- as.tnet(net, type = "weighted one-mode tnet")
if (attributes(net)$tnet != "weighted one-mode tnet")
stop("Network not loaded properly")
net[, "w"] <- net[, "w"]^alpha
if (is.null(precomp.dist)) {
if (is.null(directed)) {
tmp <- symmetrise_w(net, method = "MAX")
directed <- (nrow(tmp) != nrow(net) | sum(tmp[, "w"]) !=
sum(net[, "w"]))
}
precomp.dist <- distance_w(net = net, directed = directed,
gconly = gconly)
}
precomp.dist[is.infinite(precomp.dist)] <- NA
out <- cbind(node = attributes(precomp.dist)$nodes, closeness = rowSums(precomp.dist,
na.rm = TRUE), n.closeness = NaN)
out[, "closeness"] <- 1/out[, "closeness"]
out[, "n.closeness"] <- out[, "closeness"]/(nrow(out) – 1)
return(out)
}
What do you think could have caused the problem? I’m looking forward to your answer! Thanks a lot!
Janet
34.
Janet | November 8, 2012 at 3:02 pm
Sorry, somehow the code I inputted disappeared during posting. I tried your example as below:
It seems that the algorithm is doing the inverse(sum(distance)) instead of the sum(inverse(distance))
Could it be that the function was changed at some point? Thanks!
> net
> closeness_w(net, alpha = 1,gconly=FALSE)
And the result is:
node closeness n.closeness
[1,] 1 0.08333333 0.008333333
[2,] 2 0.10000000 0.010000000
[3,] 3 0.11111111 0.011111111
[4,] 4 0.11111111 0.011111111
[5,] 5 0.09090909 0.009090909
[6,] 6 0.09090909 0.009090909
[7,] 7 0.07142857 0.007142857
[8,] 8 Inf Inf
[9,] 9 0.33333333 0.033333333
[10,] 10 0.50000000 0.050000000
[11,] 11 0.33333333 0.033333333
35.
Tore Opsahl | November 8, 2012 at 3:42 pm
Hi Janet,
Thank you for discovering this bug. There seems to have been a recent update that broke it. I have updated the code, and will publish a new version of tnet. In the meantime, send me an email, and I can send you the code.
Tore
36.
Stefan | February 28, 2013 at 4:48 pm
Dear Tore,
As my networks sometimes consist of multiple components I used the proposed normalized closeness measure. Would you have a scientific journal article reference where I can refer to?
Thanks,
Stefan
37.
Tore Opsahl | February 28, 2013 at 5:19 pm
Hi Stefan,
Glad you found it useful. It is mentioned in my Node centrality in weighted networks: Generalizing degree and shortest paths-paper.
Thanks,
Tore
38.
Leila | May 26, 2013 at 9:42 am
Hi Tore,
I send you my databank on your personal address. You may have received it as “spam”. It doesn’t matter. I have just one question. In the case of directed networks, how can I use the option type “in” or type “out” for the closeness indicators. While this option works for the degree it does not work for the closeness.
Do you have an idea how to solve this problem ?
Again, thank you very much for your help and your research !
Leila
39.
Leila | May 28, 2013 at 12:42 pm
Hi Tore,
I have just come to understand my mystake by analyzing the distance function. Again, Thank you for your excellent research !
Leila
40.
Tania | June 18, 2013 at 12:09 am
I want to use your closeness centrality in networks with disconnected components. Do you have an article published with it or should I cite this website? I checked your 2010 paper but the algorithm is different.
Thanks,
Tania
41.
Tore Opsahl | June 18, 2013 at 4:24 pm
Hi Tania,
The main closeness algorithm in the paper is indeed different, but the work-around elaborated on here is mentioned in footnote 1.
Hope this helps,
Tore
42.
Jinie Pak | July 17, 2013 at 6:31 pm
Hi Tore,
I got kind of confused about reading the closeness outputs.
I used different alpha values for comparing outputs.
Which one is the weighted closeness score for each alpha- closeness or n.closeness ?
Cause depending on the alpha value, these two scores keep changing.
Thank you!
Jinie
43.
Tore Opsahl | July 19, 2013 at 12:48 am
Hi Jinie,
Did you specify measure=”alpha” as well as setting the alpha parameter different from 1?
The measure-parameter decides which columns are outputted.
Best,
Tore
44.
Tore Opsahl | June 3, 2014 at 12:09 pm
If anyone needs a more memory efficient version of the code, see https://toreopsahl.com/2010/04/21/article-node-centrality-in-weighted-networks-generalizing-degree-and-shortest-paths/#comment-112804
# To speed thing up, you might want to enable JIT compiling library(compiler) enableJIT(3) # Load tnet library(tnet) # Load sample network from blog post net <- cbind( i=c(1,1,2,2,2,3,3,3,4,4,4,5,5,6,6,7,9,10,10,11), j=c(2,3,1,3,5,1,2,4,3,6,7,2,6,4,5,4,10,9,11,10), w=c(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1)) # New function closeness_w2 <- function (net, directed = NULL, gconly = TRUE, alpha = 1) { if (is.null(attributes(net)$tnet)) net <- as.tnet(net, type = "weighted one-mode tnet") if (attributes(net)$tnet != "weighted one-mode tnet") stop("Network not loaded properly") net[, "w"] <- net[, "w"]^alpha if (is.null(directed)) { tmp <- symmetrise_w(net, method = "MAX") directed <- (nrow(tmp) != nrow(net) | sum(tmp[, "w"]) != sum(net[, "w"])) } # From distance_w-function g <- tnet_igraph(net, type = "weighted one-mode tnet", directed = directed) if (gconly) { stop("This code is only tested on gconly=FALSE") } else { gc <- as.integer(V(g)) } # Closeness scores out <- sapply(gc, function(a) { row <- as.numeric(igraph::shortest.paths(g, v=a, mode = "out", weights = igraph::get.edge.attribute(g,"tnetw"))) return(sum(1/row[row!=0])) }) out <- cbind(node = gc, closeness = out, n.closeness = out/(length(out) - 1)) return(out) } # JIT compiled closeness_w2c <- cmpfun(closeness_w2) # Scores with old function closeness_w(net, gconly=FALSE) # Scores with new function (regular and compiled) closeness_w2(net, gconly=FALSE) closeness_w2c(net, gconly=FALSE) # Disable JIT compiling enableJIT(0)Hope this helps!
Tore
45.
giannhs90 | June 7, 2014 at 1:29 pm
Hi Tore,
I have the same problem with Leila
” In the case of directed networks, how can I use the option type “in” or type “out” for the closeness indicators. While this option works for the degree it does not work for the closeness.
Do you have an idea how to solve this problem ?”
Your function calculates the “outcoming” paths of a node. What can i do if i am interested in closeness centrality as an “incoming” measure?
46.
Tore Opsahl | June 7, 2014 at 1:55 pm
Hi,
This would require transposing the distance matrix. You can calculate the distance matrix using the distance_w-function (eg dmat <- distance_w(net)), transpose it (tdmat <- t(dmat)), and then supply this matrix as the precomputed distance matrix to the closeness_w-function.
Hope this helps,
Tore
47.
giannhs90 | June 7, 2014 at 5:27 pm
The things you said, it was something that i almost knew .I have changed the code and i found the result i wanted. I just wondered if there was a way to create this by simple changing one variable in the closeness_W function.
Thank you so much for replying
Giannhs90
48.
Sean Everton | December 12, 2014 at 6:59 pm
Hello:
I just ran across this, so I apologize for coming a bit late to the part, but Borgatti (2006) — “Identifying sets of key players in a social network” — uses average reciprocal distance as an alternative closeness measure. It has also been implemented in UCINET for some time, possibly dating back to 2006 or earlier, but I don’t know for sure.
49.
Tore Opsahl | December 14, 2014 at 3:20 am
Thanks for this reference, Sean. There is a whole host of centrality metrics, and this site does not attempt to be a complete source. This post is simply highlighting that it’s possible to calculate closeness centrality on disconnected networks.
Do you get similar scores for the sample network above in UCINET?
Tore
50.
vivek | September 18, 2016 at 3:00 am
Hi Tore, I am using tnet for one of my project using tnet. While implementing it, I was unclear about the interpretation of it for weighted network. I was wondering if closeness(normalised) is close to 1 does it mean that the node is more central than a node with value less than 1. How does the correlation works out to be with degree as in, if a node has very high degree, will the closeness be also high. Thanks for clarification.
51.
Tore Opsahl | September 20, 2016 at 3:10 am
Hi Vivek,
The “normalizations” do not have a max value for weighted networks as there is no max value. See comment #27 on this page on why I don’t think normalizations are appropriate: https://toreopsahl.com/tnet/weighted-networks/node-centrality/
There tends to be a positive correlation between degree and closeness (i.e., a high degree node tends to be closer to all the other nodes) in real-world networks.
Best,
Tore
52.
Divya Lekha | October 19, 2016 at 2:12 am
Hi Tore
I am new to the area of large networks. I have been reading on centrality measures. And came across your article. I was wondering if the closeness centrality measure is similar to median computation in graph theory.
Median problem is a very important facility location model. Have you come across any paper on median computation in large networks? If you have, please suggest some references.
Thank you
regards
Divya
53.
Tore Opsahl | October 26, 2016 at 5:01 pm
Hi Divya,
I am not familiar with median computation in graph theory. Closeness is the inverse sum of distances to all other nodes in a network.
Good luck!
Tore
54.
Danny | August 31, 2018 at 4:15 am
Hey!
How can I calculate the “intra-component” closeness centrality (of networks with two components) in R?
R said me: “[1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0” if i want to calculate the closeness centrality of a network with two components.
Thank you for the help!
55.
Tore Opsahl | August 31, 2018 at 4:37 pm
Hi Danny,
You can extract the components using a package like igraph, and then run the closeness_w-function. I would advice against it though. The values in a smaller component will be on average closer than those in a large component simply because there are fewer paths. I would rather suggest setting the gconly parameter to FALSE instead. See the post above.
Best,
Tore
56.
Dean Hirschmann | November 1, 2020 at 6:37 am
Hi Tore,
i am analyzing a unweighted, directed network of companies and try to perform some network indicators like betweenness, in – and outdegree and closeness.
I have already figured out that my network have many individual components, so R shows me this:
`
closeness2019 <- data.frame(closeness(links2019, mode = c("all"), weights = NULL, normalized = TRUE))
Warning message:
In closeness(links2019, mode = c("all"), weights = NULL, normalized = TRUE) :
At centrality.c:2784 :closeness centrality is not well-defined for disconnected graphs
`
Then I found your `tnet`-Package and tried to calculate the closeness for the individual components but i receive and error:
`
closeness_w(links2019, gconly = FALSE)
Error in if (NC == 2) net <- data.frame(tmp[, 1], tmp[, 2]) :
argument is of length zero
`
Do you have an idea what might go wrong?
57.
Dean Hirschmann | November 1, 2020 at 11:00 am
Hi Tore,
i am analyzing an unweighted, directed network of companies. My data has just two vectors. The first with the output nodes and in the second the companies there are linked to.
I already figured out that it has many single components. So i tried to calculate the closeness for disconnected graphs in my network with your tnet package.
But R shows me this error:
Error in if (NC == 2) net <- data.frame(tmp[, 1], tmp[, 2]) :
argument is of length zero
Do you have any idea how to fix it?
58.
Tore Opsahl | November 4, 2020 at 11:17 am
Hi Dean,
You should add a third column with all 1s to make it an unweighted network. Otherwise, it will assume that it’s a two mode network.
Best,
Tore
59.
Darcy | February 2, 2024 at 8:35 am
Hi Tore,
I would like to ask if your closeness centrality approach can be directly implemented in Matlab. If so, could you provide some guidance or code examples on how to implement this method in Matlab?
Best,
Darcy