Average shortest distance in weighted networks
January 9, 2009 at 12:00 am 8 comments
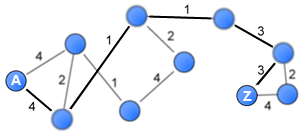The average distance that separate nodes in a network became a famous measure following Milgram’s six-degrees of separation experiment in 1967 that found that people in the US were on average 6-steps from each other. This post proposes a generalisation of this measure to weighted networks by building on work by Dijkstra (1959) and Newman (2001).
The content of this post has been integrated in the tnet manual, see Shortest Paths in Weighted Networks.
Entry filed under: Network thoughts. Tags: centrality, closeness, complex networks, global, graphs, network, shortest distance, social network analysis, valued networks, weighted networks.
RSS feed
Tore Opsahl 
1.
esagor | January 9, 2009 at 2:46 pm
Tore, this is great stuff. I’m also working on dissertation research (pretty early in the process) and love the way you’ve organized your site. I look forward to reading future posts and seeing how your work proceeds.
2.
kaikuo | May 5, 2009 at 12:36 pm
your posts are really helpful:) I am working on my dissertation too
3.
Jacob | March 31, 2010 at 8:15 pm
I am an old sociologist, returning to social network analysis after 35 years (in the early 1970-ies we called it sociometry). I too, find your site most helpful, and look forward to using your tnet.
Best regards,
Jacob
4.
Danielle | January 20, 2011 at 4:13 pm
I have a question. The last picture and the table are not synchronizing. Because this transformation is to invert the weights, I think the values have to be 2.33/4, 2.33/2, and 2.33/1, not 4/2.33 etc. What do you think?
5.
Tore Opsahl | January 21, 2011 at 1:28 pm
Danielle,
You are absolutely correct. The values should have been the other way around. Will upload a new diagram soon.
Tore
6.
sadia shah | May 1, 2011 at 11:45 am
Tore,
I am greatly thankful to u for these posts….they have helped me a lot…..to add to it,can u do the following confirmations about this article?
1-In your solution for graphs with disconnected components you used inversed distances and for the normalized closeness you use the following definition,
sum of all inversed distance/number of nodes-1
is it applicable here for weighted networks too? i think it is but again need your opinion too.
2- Also tell me will it be safe to use this solution for directed plus weighted networks where e.g. a route from A to C via B exists but no route from C to A exist via B? I dont think there is any harm in it but still need your opinion.
3- When u suggest to “normalise” the weights by the average weight in the above network, u calculate it to be (4+4+2+2+1+1)/6=2.33………are u using the number of links(6) or the number of nodes(6) in the denominator? i think it is the number of links but still need your confirmation.
4-in the last diagram, weights should be like this 2.33/x and not like this x/2.33……..am i right?
waiting for an urgent reply……it wil be v helpful indeed
Regards,
Sadia.
7.
Tore Opsahl | May 1, 2011 at 4:09 pm
Sadia,
Thank you for taking such a strong interest in the blog posts.
1) The normalisation of the closeness for weighted networks does not force the measure to be between 0 and 1. As a theoretical maximum value is not defined, it is not possible to divide the non-normalised scores by such a value. See these comments for more information on why I don’t think normalisation is appropriate (one;two).
2) All the one-mode measures in tnet, except the local clustering coefficient, are designed to be applicable to directed networks as well as undirected networks, including this one.
3) To get the average weight, you sum the tie weights and divide by number of ties.
4) This diagram was supposed to highlight how the tie weights are altered before they are inverted. I have clarified this above now. Whether they are “normalised” or inverted first is irrelevant.
Hope this helps,
Tore
8.
sadia shah | May 2, 2011 at 6:31 am
thank u so much……..u made my day:)