Posts tagged ‘strength of ties’
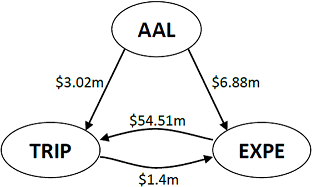 Networks has the potential to increase the explanatory power of models. The content of this post, and accompanying paper, quantifies the size of this effect for predicting the financial health of companies. It is my hope that it can help drive more research into networks and enable more organizations to develop better models and understand interdependencies to a greater extent.
Networks has the potential to increase the explanatory power of models. The content of this post, and accompanying paper, quantifies the size of this effect for predicting the financial health of companies. It is my hope that it can help drive more research into networks and enable more organizations to develop better models and understand interdependencies to a greater extent.
Companies do not operate in a vacuum. As companies move towards an increasingly specialized production function and their reach is becoming truly global, their aptitude in managing and shaping their inter-organizational network is a determining factor in measuring their health. Current models of company financial health often lack variables explaining the inter-organizational network, and as such, assume that (1) all networks are the same and (2) the performance of partners do not impact companies. This paper aims to be a first step in the direction of removing these assumptions. Specifically, the impact is illustrated by examining the effects of customer and supplier concentrations and partners’ credit risk on credit-default swap (CDS) spreads while controlling for credit risk and size. We rely upon supply-chain data from Bloomberg that provides insight into companies’ relationships. The empirical results show that a well diversified customer network lowers CDS spread, while having stable partners with low default probabilities increase spreads. The latter result suggests that successful companies do not focus on building a stable eco-system around themselves, but instead focus on their own profit maximization at the cost of the financial health of their suppliers’ and customers’. At a more general level, the results indicate the importance of considering the inter-organizational networks, and highlight the value of including network variables in credit risk models.
Continue Reading February 23, 2016 at 1:20 am
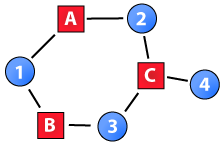 A paper called “Triadic closure in two-mode networks: Redefining the global and local clustering coefficients” that I have authored will be published in the special issue of Social Networks on two-mode networks (2012).
A paper called “Triadic closure in two-mode networks: Redefining the global and local clustering coefficients” that I have authored will be published in the special issue of Social Networks on two-mode networks (2012).
As the vast majority of network measures are defined for one-mode networks, two-mode networks often have to be projected onto one-mode networks to be analyzed. A number of issues arise in this transformation process, especially when analyzing ties among nodes’ contacts. For example, the values attained by the global and local clustering coefficients on projected random two-mode networks deviate from the expected values in corresponding classical one-mode networks. Moreover, both the local clustering coefficient and constraint (structural holes) are inversely associated to nodes’ two-mode degree. To overcome these issues, this paper proposes redefinitions of the clustering coefficients for two-mode networks.
Continue Reading December 21, 2011 at 9:00 am
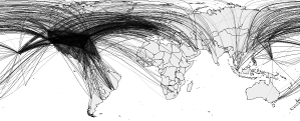 A surprising finding when analysing airport networks is the importance of Anchorage airport in Alaska. In fact, it is the most central airport in the network when applying betweenness! I do not believe this finding is completely accurate due to two reasons: (1) there is a potential for measurement error when not including tie weights (i.e., assigning the same importance to the connection between London Heathrow and New York’s JFK as to the connection between Pack Creek Airport and Sitka Harbor Sea Plane Base in Alaska), and (2) relying on US data only leads to sample selection as the airport network is a global system. This post highlights how to use a weighted betweenness measure as well as the extent of the sample selection issue.
A surprising finding when analysing airport networks is the importance of Anchorage airport in Alaska. In fact, it is the most central airport in the network when applying betweenness! I do not believe this finding is completely accurate due to two reasons: (1) there is a potential for measurement error when not including tie weights (i.e., assigning the same importance to the connection between London Heathrow and New York’s JFK as to the connection between Pack Creek Airport and Sitka Harbor Sea Plane Base in Alaska), and (2) relying on US data only leads to sample selection as the airport network is a global system. This post highlights how to use a weighted betweenness measure as well as the extent of the sample selection issue.
Continue Reading August 12, 2011 at 1:39 am
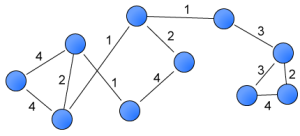
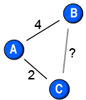
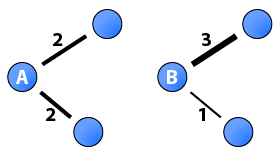 A central metric in network research is the number of ties each node has, degree. Degree has been generalised to weighted networks as the sum of tie weights (Barrat et al., 2004), and as a function of the number of ties and the sum of their weights (Opsahl et al., 2010). However, all these measures are insensitive to variation in the tie weights. As such, the two nodes in this diagram would always have the same degree score. This post showcases a new measure that uses a tuning parameter to control whether variation should be taken favourable or discount the degree centrality score of a focal node.
A central metric in network research is the number of ties each node has, degree. Degree has been generalised to weighted networks as the sum of tie weights (Barrat et al., 2004), and as a function of the number of ties and the sum of their weights (Opsahl et al., 2010). However, all these measures are insensitive to variation in the tie weights. As such, the two nodes in this diagram would always have the same degree score. This post showcases a new measure that uses a tuning parameter to control whether variation should be taken favourable or discount the degree centrality score of a focal node.
Continue Reading August 8, 2011 at 11:28 pm
 A paper called “Node centrality in weighted networks: Generalizing degree and shortest paths” that I have co-authored will be published in Social Networks. Ties often have a strength naturally associated with them that differentiate them from each other. Tie strength has been operationalized as weights. A few network measures have been proposed for weighted networks, including three common measures of node centrality: degree, closeness, and betweenness. However, these generalizations have solely focused on tie weights, and not on the number of ties, which was the central component of the original measures. This paper proposes generalizations that combine both these aspects. We illustrate the benefits of this approach by applying one of them to Freeman’s EIES dataset.
A paper called “Node centrality in weighted networks: Generalizing degree and shortest paths” that I have co-authored will be published in Social Networks. Ties often have a strength naturally associated with them that differentiate them from each other. Tie strength has been operationalized as weights. A few network measures have been proposed for weighted networks, including three common measures of node centrality: degree, closeness, and betweenness. However, these generalizations have solely focused on tie weights, and not on the number of ties, which was the central component of the original measures. This paper proposes generalizations that combine both these aspects. We illustrate the benefits of this approach by applying one of them to Freeman’s EIES dataset.
Continue Reading April 21, 2010 at 10:37 am
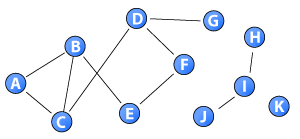 A key node centrality measure in networks is closeness centrality (Freeman, 1978; Wasserman and Faust, 1994). It is defined as the inverse of farness, which in turn, is the sum of distances to all other nodes. As the distance between nodes in disconnected components of a network is infinite, this measure cannot be applied to networks with disconnected components (Opsahl et al., 2010; Wasserman and Faust, 1994). This post highlights a possible work-around, which allows the measure to be applied to these networks and at the same time maintain the original idea behind the measure.
A key node centrality measure in networks is closeness centrality (Freeman, 1978; Wasserman and Faust, 1994). It is defined as the inverse of farness, which in turn, is the sum of distances to all other nodes. As the distance between nodes in disconnected components of a network is infinite, this measure cannot be applied to networks with disconnected components (Opsahl et al., 2010; Wasserman and Faust, 1994). This post highlights a possible work-around, which allows the measure to be applied to these networks and at the same time maintain the original idea behind the measure.
Continue Reading March 20, 2010 at 1:03 pm
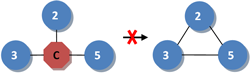 Similar to the motivation of the global clustering coefficient that I proposed in Clustering in two-mode networks, the local clustering coefficient is biased if applied to a projection of a two-mode network. It is biased in the sense that the randomly expected value is not obtained on the projection of a random two-mode network. To overcome this methodological bias, I redefine the local clustering coefficient for two-mode networks. The new coefficient is a mix between the global clustering coefficient for two-mode networks and Barrat’s (2004) local coefficient for a weighted one-mode network. The coefficient is tested on Davis’ (1940) Southern Women dataset.
Similar to the motivation of the global clustering coefficient that I proposed in Clustering in two-mode networks, the local clustering coefficient is biased if applied to a projection of a two-mode network. It is biased in the sense that the randomly expected value is not obtained on the projection of a random two-mode network. To overcome this methodological bias, I redefine the local clustering coefficient for two-mode networks. The new coefficient is a mix between the global clustering coefficient for two-mode networks and Barrat’s (2004) local coefficient for a weighted one-mode network. The coefficient is tested on Davis’ (1940) Southern Women dataset.
January 6, 2010 at 6:29 pm
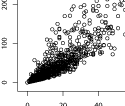 This post explores the relationship between node degree and node strength in an online social network. In the online social network, heterogeneity in nodes’ average tie weight across different levels of degree had been reported
This post explores the relationship between node degree and node strength in an online social network. In the online social network, heterogeneity in nodes’ average tie weight across different levels of degree had been reported . Although degree and average tie weight are significantly correlated, this post argues for the similarity of degree and node strength. In particular, high pair-wise correlation between degree and strength is found. In addition, power-law exponents of degree distributions and strength distribution are reported. The exponents are strikingly similar, in fact, they are almost identical.
. Although degree and average tie weight are significantly correlated, this post argues for the similarity of degree and node strength. In particular, high pair-wise correlation between degree and strength is found. In addition, power-law exponents of degree distributions and strength distribution are reported. The exponents are strikingly similar, in fact, they are almost identical.
Continue Reading October 16, 2009 at 12:57 pm
 Many network dataset are by definition two-mode networks. Yet, few network measures can be directly applied to them. Therefore, two-mode networks are often projected onto one-mode networks by selecting a node set and linking two nodes if they were connected to common nodes in the two-mode network. This process has a major impact on the level of clustering in the network. If three or more nodes are connected to a common node in the two-mode network, the nodes form a fully-connected clique consisting of one or more triangles in the one-mode projection. Moreover, it produces a number of modeling issues. For example, even a one-mode projection of a random two-mode network with same number of nodes and ties will have a higher clustering coefficient than the randomly expected value. This post represents an attempt to overcome this issue by redefining the clustering coefficient so that it can be calculated directly on the two-mode structure. I illustrate the benefits of such an approach by applying it to two-mode networks from four different domains: event attendance, scientific collaboration, interlocking directorates, and online communication.
Many network dataset are by definition two-mode networks. Yet, few network measures can be directly applied to them. Therefore, two-mode networks are often projected onto one-mode networks by selecting a node set and linking two nodes if they were connected to common nodes in the two-mode network. This process has a major impact on the level of clustering in the network. If three or more nodes are connected to a common node in the two-mode network, the nodes form a fully-connected clique consisting of one or more triangles in the one-mode projection. Moreover, it produces a number of modeling issues. For example, even a one-mode projection of a random two-mode network with same number of nodes and ties will have a higher clustering coefficient than the randomly expected value. This post represents an attempt to overcome this issue by redefining the clustering coefficient so that it can be calculated directly on the two-mode structure. I illustrate the benefits of such an approach by applying it to two-mode networks from four different domains: event attendance, scientific collaboration, interlocking directorates, and online communication.
September 11, 2009 at 12:00 am
 tnet is a package written in R that can calculate weighted social network measures. Almost all of the ideas posted on this blog are related to weighted networks as, I believe, taking into consideration tie weights enables us to uncover and study interesting network properties. Not only are few social network measures applicable to weighted networks, but there is also a lack of software programmes that can analyse this type of networks. In fact, there are no open-source programmes. This hinders the use and development of weighted measures. tnet represents a first step towards creating such a programme. Through this platform, weighted network measures can easily be applied, and new measures easily implemented and distributed.
tnet is a package written in R that can calculate weighted social network measures. Almost all of the ideas posted on this blog are related to weighted networks as, I believe, taking into consideration tie weights enables us to uncover and study interesting network properties. Not only are few social network measures applicable to weighted networks, but there is also a lack of software programmes that can analyse this type of networks. In fact, there are no open-source programmes. This hinders the use and development of weighted measures. tnet represents a first step towards creating such a programme. Through this platform, weighted network measures can easily be applied, and new measures easily implemented and distributed.
The content of this post has been integrated in the
tnet manual, see
Software.
June 12, 2009 at 12:00 am
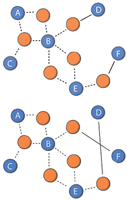 In this post, I extend the Weighted Rich-club Effect by suggesting and testing a different null model for the scientific collaboration network (Newman, 2001). This network is a two-mode network, which becomes an undirected one-mode network when projected. In the paper, we compared the observed weighted rich-club coefficient with the one found on random networks. The random networks were constructed by a null model defined for directed networks when prominence was based on node strength. Therefore, we created a directed network from the undirected scientific collaboration network by linking connected nodes with two directed ties that had the same weight. The null model consisted in reshuffling the tie weights attached to out-going ties for each node. However, this local reshuffling broke the weight symmetry of the two directed ties between connected nodes. The null model proposed in this post is based on the randomisation of the two-mode network before projecting it onto a one-mode network. By randomising before projecting, we are able to randomise a network while keeping the symmetry of weights.
In this post, I extend the Weighted Rich-club Effect by suggesting and testing a different null model for the scientific collaboration network (Newman, 2001). This network is a two-mode network, which becomes an undirected one-mode network when projected. In the paper, we compared the observed weighted rich-club coefficient with the one found on random networks. The random networks were constructed by a null model defined for directed networks when prominence was based on node strength. Therefore, we created a directed network from the undirected scientific collaboration network by linking connected nodes with two directed ties that had the same weight. The null model consisted in reshuffling the tie weights attached to out-going ties for each node. However, this local reshuffling broke the weight symmetry of the two directed ties between connected nodes. The null model proposed in this post is based on the randomisation of the two-mode network before projecting it onto a one-mode network. By randomising before projecting, we are able to randomise a network while keeping the symmetry of weights.
May 29, 2009 at 12:00 am
I have now completed my Ph.D. at the School of Business and Management of Queen Mary College, University of London. My Ph.D. programme was defined around a number of projects, which drew on, and extended, recent theoretical and methodological advances in network science. The projects that were concerned with weighted networks and longitudinal networks were outlined and critically discussed in my thesis (Structure and Evolution of Weighted Networks). The entire thesis, except Appendix C which is outdated, is available on the Publication > Thesis-page.
Acknowledgements
The theme of this thesis is interdependence among elements. In fact, this thesis is not just a product of myself, but also of my interdependence with others. Without the support of a number of people, it would not have been possible to write. It is my pleasure to have the opportunity to express my gratitude to many of them here.
For my academic achievements, I would like to acknowledge the constant support from my supervisors. In particular, I thank Pietro Panzarasa for taking an active part of all the projects I have worked on. I have also had the pleasure to collaborate with people other than my supervisors. I worked with Vittoria Colizza and Jose J. Ramasco on the analysis and method presented in Chapter 2, Kathleen M. Carley on an empirical analysis of the online social network used throughout this thesis, and Martha J. Prevezer on a project related to knowledge transfer in emerging countries. In addition to these direct collaborations, I would also like to thank Filip Agneessens, Sinan Aral, Steve Borgatti, Ronald Burt, Mauro Faccioni Filho, Thomas Friemel, John Skvoretz, and Vanina Torlo for encouragement and helpful advice. In particular, I would like to thank Tom A. B. Snijders and Klaus Nielsen for insightful reading of this thesis and many productive remarks and suggestions. I have also received feedback on my work at a number of conferences and workshops. I would like to express my gratitude to the participants at these.
On a social note, I would like to thank John, Claudius, and my family for their continuing support. Without them I would have lost focus. My peers and the administrative staff have also been a great source of support. In particular, I would like to extend my acknowledgements to Mariusz Jarmuzek, Geraldine Marks, Roland Miller, Jenny Murphy, Cathrine Seierstad, Lorna Soar, Steven Telford, and Eshref Trushin.
May 15, 2009 at 12:00 am
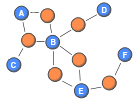 This post highlights a number of methods for projecting both binary and weighted two-mode networks (also known as affiliation or bipartite networks) onto weighted one-mode networks. Although I would prefer to analyse two-mode networks in their original form, few methods exist for that purpose. These networks can be transformed into one-mode networks by projecting them (i.e., selecting one set of nodes, and linking two nodes if they are connected to the same node of the other set). Traditionally, ties in the one-mode networks are without weights. By carefully considering multiple ways of projecting two-mode networks onto weighted one-mode networks, we can maintain some of the richness contained within the two-mode structure. This enables researchers to conduct a deeper analysis than if the two-mode structure was completely ignored.
This post highlights a number of methods for projecting both binary and weighted two-mode networks (also known as affiliation or bipartite networks) onto weighted one-mode networks. Although I would prefer to analyse two-mode networks in their original form, few methods exist for that purpose. These networks can be transformed into one-mode networks by projecting them (i.e., selecting one set of nodes, and linking two nodes if they are connected to the same node of the other set). Traditionally, ties in the one-mode networks are without weights. By carefully considering multiple ways of projecting two-mode networks onto weighted one-mode networks, we can maintain some of the richness contained within the two-mode structure. This enables researchers to conduct a deeper analysis than if the two-mode structure was completely ignored.
May 1, 2009 at 12:00 am
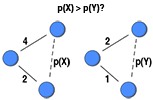 A key assumption of Granovetter’s (1973) Strength of Weak Ties theory is that strong ties are embedded by being part of triangles, whereas weak ties are not embedded by being created towards disconnected nodes. This assumption have been tested by calculating the traditional clustering coefficient on binary networks created with increasing cut-off parameters (i.e., creating a series of binary networks from a weighted network where ties with a weight greater than a cut-off parameter is set to present and the rest removed). Contrarily to theories of strong ties and embeddedness, these methods generally showed that the clustering coefficient decreased as the cut-off parameter increased. However, the binary networks were not comparable with each other as they had a different number of ties. Another way of testing this assumption is to take the ratio between the weighted global clustering coefficient and the traditional coefficient measured on networks where all ties are considered present. Thus, the number of ties is maintained. This post highlights this feature and empirically tests it on a number of publically available weighted network datasets.
A key assumption of Granovetter’s (1973) Strength of Weak Ties theory is that strong ties are embedded by being part of triangles, whereas weak ties are not embedded by being created towards disconnected nodes. This assumption have been tested by calculating the traditional clustering coefficient on binary networks created with increasing cut-off parameters (i.e., creating a series of binary networks from a weighted network where ties with a weight greater than a cut-off parameter is set to present and the rest removed). Contrarily to theories of strong ties and embeddedness, these methods generally showed that the clustering coefficient decreased as the cut-off parameter increased. However, the binary networks were not comparable with each other as they had a different number of ties. Another way of testing this assumption is to take the ratio between the weighted global clustering coefficient and the traditional coefficient measured on networks where all ties are considered present. Thus, the number of ties is maintained. This post highlights this feature and empirically tests it on a number of publically available weighted network datasets.
The content of this post has been integrated in the
tnet manual, see
Clustering.
April 17, 2009 at 12:00 am
 A paper called “Clustering in Weighted Networks” that I have co-authored will be published in Social Networks. Although many social network measures exist for binary networks and many theories differentiate between strong and weak ties, few measures have been generalised so that they can be applied to weighted networks and retain the information encoded in the weights of ties. One of these measures is the global clustering coefficient, which measures embeddedness or, more specifically, the likelihood of a triplet being closed by a tie so that it forms a triangle. This article proposes a generalisation of this key network measure to weighted networks.
A paper called “Clustering in Weighted Networks” that I have co-authored will be published in Social Networks. Although many social network measures exist for binary networks and many theories differentiate between strong and weak ties, few measures have been generalised so that they can be applied to weighted networks and retain the information encoded in the weights of ties. One of these measures is the global clustering coefficient, which measures embeddedness or, more specifically, the likelihood of a triplet being closed by a tie so that it forms a triangle. This article proposes a generalisation of this key network measure to weighted networks.
Continue Reading April 3, 2009 at 12:00 am
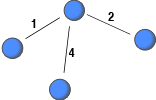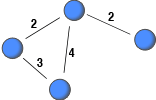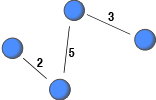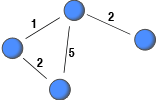 Recently, a number of network dataset have been constructed from archival data (e.g., email logs) with the aim to study human interaction. This has allowed researchers to study large-scale social networks. If the archival data does not included information about the severing or weakening of ties, non-relevant interaction among people, which occurred far in the past, might be deemed relevant. This post highlights this issue and suggests imposing a lifespan on interactions to record only relevant ties with the current strength.
Recently, a number of network dataset have been constructed from archival data (e.g., email logs) with the aim to study human interaction. This has allowed researchers to study large-scale social networks. If the archival data does not included information about the severing or weakening of ties, non-relevant interaction among people, which occurred far in the past, might be deemed relevant. This post highlights this issue and suggests imposing a lifespan on interactions to record only relevant ties with the current strength.
The content of this post has been integrated in the
tnet manual, see
Sliding Window.
March 20, 2009 at 12:00 am
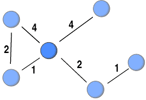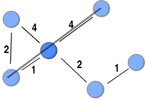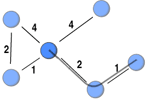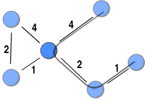 This post highlights a generalisation of Freeman’s (1978) betweenness measure to weighted networks implicitly introduced by Brandes (2001) when he developed an algorithm for calculating betweenness faster. Betweenness is a measure of the extent to which a node funnels transactions among all the other nodes in the network. By funnelling the transactions, a node can broker. This could be by taking a cut (e.g. Ukraine controls most gas pipelines from Russia to Europe) or distorting the information being transmitted to its advantage.
This post highlights a generalisation of Freeman’s (1978) betweenness measure to weighted networks implicitly introduced by Brandes (2001) when he developed an algorithm for calculating betweenness faster. Betweenness is a measure of the extent to which a node funnels transactions among all the other nodes in the network. By funnelling the transactions, a node can broker. This could be by taking a cut (e.g. Ukraine controls most gas pipelines from Russia to Europe) or distorting the information being transmitted to its advantage.
February 20, 2009 at 12:00 am
A paper called Prominence and control: The weighted rich-club effect that I have co-authored was published in Physical Review Letters (PRL). In this paper, we proposed a new general framework for studying the tendency of prominent nodes to direct their strongest ties toward each other.
Continue Reading December 12, 2008 at 12:00 am
 Networks are the cornerstone of this blog, therefore I have decided to make the first post my definition of a network and a few basic network measures.
Networks are the cornerstone of this blog, therefore I have decided to make the first post my definition of a network and a few basic network measures.
The content of this post has been integrated in the
tnet manual.
November 28, 2008 at 12:00 am
 Networks has the potential to increase the explanatory power of models. The content of this post, and accompanying paper, quantifies the size of this effect for predicting the financial health of companies. It is my hope that it can help drive more research into networks and enable more organizations to develop better models and understand interdependencies to a greater extent.
Networks has the potential to increase the explanatory power of models. The content of this post, and accompanying paper, quantifies the size of this effect for predicting the financial health of companies. It is my hope that it can help drive more research into networks and enable more organizations to develop better models and understand interdependencies to a greater extent. A surprising finding when analysing airport networks is the importance of Anchorage airport in Alaska. In fact, it is the most central airport in the network when applying betweenness! I do not believe this finding is completely accurate due to two reasons: (1) there is a potential for measurement error when not including tie weights (i.e., assigning the same importance to the connection between London Heathrow and New York’s JFK as to the connection between Pack Creek Airport and Sitka Harbor Sea Plane Base in Alaska), and (2) relying on US data only leads to sample selection as the airport network is a global system. This post highlights how to use a weighted betweenness measure as well as the extent of the sample selection issue.
A surprising finding when analysing airport networks is the importance of Anchorage airport in Alaska. In fact, it is the most central airport in the network when applying betweenness! I do not believe this finding is completely accurate due to two reasons: (1) there is a potential for measurement error when not including tie weights (i.e., assigning the same importance to the connection between London Heathrow and New York’s JFK as to the connection between Pack Creek Airport and Sitka Harbor Sea Plane Base in Alaska), and (2) relying on US data only leads to sample selection as the airport network is a global system. This post highlights how to use a weighted betweenness measure as well as the extent of the sample selection issue. A central metric in network research is the number of ties each node has, degree. Degree has been generalised to weighted networks as the sum of tie weights (Barrat et al., 2004), and as a function of the number of ties and the sum of their weights (Opsahl et al., 2010). However, all these measures are insensitive to variation in the tie weights. As such, the two nodes in this diagram would always have the same degree score. This post showcases a new measure that uses a tuning parameter to control whether variation should be taken favourable or discount the degree centrality score of a focal node.
A central metric in network research is the number of ties each node has, degree. Degree has been generalised to weighted networks as the sum of tie weights (Barrat et al., 2004), and as a function of the number of ties and the sum of their weights (Opsahl et al., 2010). However, all these measures are insensitive to variation in the tie weights. As such, the two nodes in this diagram would always have the same degree score. This post showcases a new measure that uses a tuning parameter to control whether variation should be taken favourable or discount the degree centrality score of a focal node. A paper called “Node centrality in weighted networks: Generalizing degree and shortest paths” that I have co-authored will be published in Social Networks. Ties often have a strength naturally associated with them that differentiate them from each other. Tie strength has been operationalized as weights. A few network measures have been proposed for weighted networks, including three common measures of node centrality: degree, closeness, and betweenness. However, these generalizations have solely focused on tie weights, and not on the number of ties, which was the central component of the original measures. This paper proposes generalizations that combine both these aspects. We illustrate the benefits of this approach by applying one of them to Freeman’s EIES dataset.
A paper called “Node centrality in weighted networks: Generalizing degree and shortest paths” that I have co-authored will be published in Social Networks. Ties often have a strength naturally associated with them that differentiate them from each other. Tie strength has been operationalized as weights. A few network measures have been proposed for weighted networks, including three common measures of node centrality: degree, closeness, and betweenness. However, these generalizations have solely focused on tie weights, and not on the number of ties, which was the central component of the original measures. This paper proposes generalizations that combine both these aspects. We illustrate the benefits of this approach by applying one of them to Freeman’s EIES dataset. A key node centrality measure in networks is closeness centrality (Freeman, 1978; Wasserman and Faust, 1994). It is defined as the inverse of farness, which in turn, is the sum of distances to all other nodes. As the distance between nodes in disconnected components of a network is infinite, this measure cannot be applied to networks with disconnected components (Opsahl et al., 2010; Wasserman and Faust, 1994). This post highlights a possible work-around, which allows the measure to be applied to these networks and at the same time maintain the original idea behind the measure.
A key node centrality measure in networks is closeness centrality (Freeman, 1978; Wasserman and Faust, 1994). It is defined as the inverse of farness, which in turn, is the sum of distances to all other nodes. As the distance between nodes in disconnected components of a network is infinite, this measure cannot be applied to networks with disconnected components (Opsahl et al., 2010; Wasserman and Faust, 1994). This post highlights a possible work-around, which allows the measure to be applied to these networks and at the same time maintain the original idea behind the measure. This post explores the relationship between node degree and node strength in an online social network. In the online social network, heterogeneity in nodes’ average tie weight across different levels of degree had been reported
This post explores the relationship between node degree and node strength in an online social network. In the online social network, heterogeneity in nodes’ average tie weight across different levels of degree had been reported . Although degree and average tie weight are significantly correlated, this post argues for the similarity of degree and node strength. In particular, high pair-wise correlation between degree and strength is found. In addition, power-law exponents of degree distributions and strength distribution are reported. The exponents are strikingly similar, in fact, they are almost identical.
. Although degree and average tie weight are significantly correlated, this post argues for the similarity of degree and node strength. In particular, high pair-wise correlation between degree and strength is found. In addition, power-law exponents of degree distributions and strength distribution are reported. The exponents are strikingly similar, in fact, they are almost identical. This post highlights a number of methods for projecting both binary and weighted two-mode networks (also known as affiliation or bipartite networks) onto weighted one-mode networks. Although I would prefer to analyse two-mode networks in their original form, few methods exist for that purpose. These networks can be transformed into one-mode networks by projecting them (i.e., selecting one set of nodes, and linking two nodes if they are connected to the same node of the other set). Traditionally, ties in the one-mode networks are without weights. By carefully considering multiple ways of projecting two-mode networks onto weighted one-mode networks, we can maintain some of the richness contained within the two-mode structure. This enables researchers to conduct a deeper analysis than if the two-mode structure was completely ignored.
This post highlights a number of methods for projecting both binary and weighted two-mode networks (also known as affiliation or bipartite networks) onto weighted one-mode networks. Although I would prefer to analyse two-mode networks in their original form, few methods exist for that purpose. These networks can be transformed into one-mode networks by projecting them (i.e., selecting one set of nodes, and linking two nodes if they are connected to the same node of the other set). Traditionally, ties in the one-mode networks are without weights. By carefully considering multiple ways of projecting two-mode networks onto weighted one-mode networks, we can maintain some of the richness contained within the two-mode structure. This enables researchers to conduct a deeper analysis than if the two-mode structure was completely ignored.  Recently, a number of network dataset have been constructed from archival data (e.g., email logs) with the aim to study human interaction. This has allowed researchers to study large-scale social networks. If the archival data does not included information about the severing or weakening of ties, non-relevant interaction among people, which occurred far in the past, might be deemed relevant. This post highlights this issue and suggests imposing a lifespan on interactions to record only relevant ties with the current strength.
Recently, a number of network dataset have been constructed from archival data (e.g., email logs) with the aim to study human interaction. This has allowed researchers to study large-scale social networks. If the archival data does not included information about the severing or weakening of ties, non-relevant interaction among people, which occurred far in the past, might be deemed relevant. This post highlights this issue and suggests imposing a lifespan on interactions to record only relevant ties with the current strength. This post highlights a generalisation of Freeman’s (1978) betweenness measure to weighted networks implicitly introduced by Brandes (2001) when he developed an algorithm for calculating betweenness faster. Betweenness is a measure of the extent to which a node funnels transactions among all the other nodes in the network. By funnelling the transactions, a node can broker. This could be by taking a cut (e.g. Ukraine controls most gas pipelines from Russia to Europe) or distorting the information being transmitted to its advantage.
This post highlights a generalisation of Freeman’s (1978) betweenness measure to weighted networks implicitly introduced by Brandes (2001) when he developed an algorithm for calculating betweenness faster. Betweenness is a measure of the extent to which a node funnels transactions among all the other nodes in the network. By funnelling the transactions, a node can broker. This could be by taking a cut (e.g. Ukraine controls most gas pipelines from Russia to Europe) or distorting the information being transmitted to its advantage.  Networks are the cornerstone of this blog, therefore I have decided to make the first post my definition of a network and a few basic network measures.
Networks are the cornerstone of this blog, therefore I have decided to make the first post my definition of a network and a few basic network measures.




 RSS feed
RSS feed