Posts tagged ‘directed networks’
Why Anchorage is not (that) important: Binary ties and Sample selection
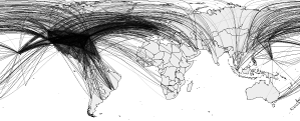A surprising finding when analysing airport networks is the importance of Anchorage airport in Alaska. In fact, it is the most central airport in the network when applying betweenness! I do not believe this finding is completely accurate due to two reasons: (1) there is a potential for measurement error when not including tie weights (i.e., assigning the same importance to the connection between London Heathrow and New York’s JFK as to the connection between Pack Creek Airport and Sitka Harbor Sea Plane Base in Alaska), and (2) relying on US data only leads to sample selection as the airport network is a global system. This post highlights how to use a weighted betweenness measure as well as the extent of the sample selection issue.
Article: Node centrality in weighted networks: Generalizing degree and shortest paths
A paper called “Node centrality in weighted networks: Generalizing degree and shortest paths” that I have co-authored will be published in Social Networks. Ties often have a strength naturally associated with them that differentiate them from each other. Tie strength has been operationalized as weights. A few network measures have been proposed for weighted networks, including three common measures of node centrality: degree, closeness, and betweenness. However, these generalizations have solely focused on tie weights, and not on the number of ties, which was the central component of the original measures. This paper proposes generalizations that combine both these aspects. We illustrate the benefits of this approach by applying one of them to Freeman’s EIES dataset.
Closeness centrality in networks with disconnected components
A key node centrality measure in networks is closeness centrality (Freeman, 1978; Wasserman and Faust, 1994). It is defined as the inverse of farness, which in turn, is the sum of distances to all other nodes. As the distance between nodes in disconnected components of a network is infinite, this measure cannot be applied to networks with disconnected components (Opsahl et al., 2010; Wasserman and Faust, 1994). This post highlights a possible work-around, which allows the measure to be applied to these networks and at the same time maintain the original idea behind the measure.
Online Social Network-dataset now available
The Online Social Network-dataset used in my Ph.D. thesis is now available on the Dataset-page. This network has also been described in Patterns and Dynamics of Users’ Behaviour and Interaction: Network Analysis of an Online Community and used in Prominence and control: The weighted rich-club effect and Clustering in weighted networks. The network originate from an online social network among students at University of California, Irvine. The edgelist includes the users that sent or received at least one message during that period (1,899). A total number of 59,835 online messages were sent among these over 20,296 directed ties.
Similarity between node degree and node strength
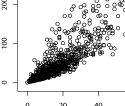This post explores the relationship between node degree and node strength in an online social network. In the online social network, heterogeneity in nodes’ average tie weight across different levels of degree had been reported
. Although degree and average tie weight are significantly correlated, this post argues for the similarity of degree and node strength. In particular, high pair-wise correlation between degree and strength is found. In addition, power-law exponents of degree distributions and strength distribution are reported. The exponents are strikingly similar, in fact, they are almost identical.
Continue Reading October 16, 2009 at 12:57 pm Leave a comment
tnet: Software for Analysing Weighted Networks
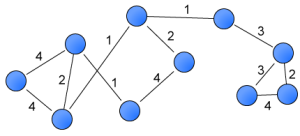tnet is a package written in R that can calculate weighted social network measures. Almost all of the ideas posted on this blog are related to weighted networks as, I believe, taking into consideration tie weights enables us to uncover and study interesting network properties. Not only are few social network measures applicable to weighted networks, but there is also a lack of software programmes that can analyse this type of networks. In fact, there are no open-source programmes. This hinders the use and development of weighted measures. tnet represents a first step towards creating such a programme. Through this platform, weighted network measures can easily be applied, and new measures easily implemented and distributed.
Article: Clustering in Weighted Networks
A paper called “Clustering in Weighted Networks” that I have co-authored will be published in Social Networks. Although many social network measures exist for binary networks and many theories differentiate between strong and weak ties, few measures have been generalised so that they can be applied to weighted networks and retain the information encoded in the weights of ties. One of these measures is the global clustering coefficient, which measures embeddedness or, more specifically, the likelihood of a triplet being closed by a tie so that it forms a triangle. This article proposes a generalisation of this key network measure to weighted networks.
Network? Weighted network?
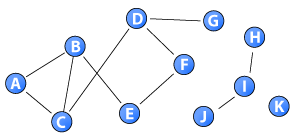
Networks are the cornerstone of this blog, therefore I have decided to make the first post my definition of a network and a few basic network measures.
RSS feed
Tore Opsahl 