Article: Clustering in Weighted Networks
April 3, 2009 at 12:00 am 7 comments
A paper called “Clustering in Weighted Networks” that I have co-authored with Pietro Panzarasa will be published in Social Networks. Unfortunately, the copyright agreement prevents me from uploading a pdf of the published paper to this blog. However, if you have access to Social Networks, you can download the paper directly. Otherwise, a preprint with the exact same text is available.
Abstract
In recent years, researchers have investigated a growing number of weighted networks where ties are differentiated according to their strength or capacity. Yet, most network measures do not take weights into consideration, and thus do not fully capture the richness of the information contained in the data. In this paper, we focus on a measure originally defined for unweighted networks: the global clustering coefficient. We propose a generalization of this coefficient that retains the information encoded in the weights of ties. We then undertake a comparative assessment by applying the standard and generalized coefficients to a number of network datasets.
Motivation
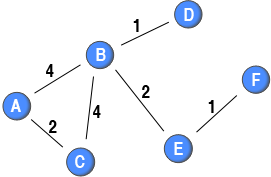 In this sample network the binary clustering coefficient is 0.33 as a third of the triplets are closed by being part of a triangle. By looking at the weights, it is possible to see that the strongest ties are in part of the closed triplets. This is not reflected in the binary clustering coefficient.
In this sample network the binary clustering coefficient is 0.33 as a third of the triplets are closed by being part of a triangle. By looking at the weights, it is possible to see that the strongest ties are in part of the closed triplets. This is not reflected in the binary clustering coefficient.
By applying the proposed generalisation of the coefficient using the arithmetic mean method for defining triplet value, the clustering coefficient increases to 0.42. This increase of this coefficient from the binary coefficient is a reflection of the fact that the strongest ties are part of the closed triplets.
Want to test it with your data?
The clustering_w function in tnet allows you to test the generalised clustering coefficient on your own dataset.
For example, to test the clustering_w function on the sample network above, you can run the following code in R:
# Load tnet
library(tnet)
# Load network
net <- cbind(
i=c(1,1,2,2,2,2,3,3,4,5,5,6),
j=c(2,3,1,3,4,5,1,2,2,2,6,5),
w=c(4,2,4,4,1,2,2,4,1,2,1,1))
# Run function
clustering_w(net, measure=c("am", "gm", "ma", "mi"))
# The output is:
# am gm ma mi
#0.4166667 0.4361302 0.3750000 0.5000000
To test in on Freeman’s third EIES network from the datasets page, you can do the following:
# Load tnet
library(tnet)
# Load network
data(Freemans.EIES)
# Run function
clustering_w(Freemans.EIES.net.3.n32, measure=c("am", "gm", "ma", "mi"))
# The output is:
#0.7378310 0.7331536 0.7410959 0.7249982
Entry filed under: Articles. Tags: arcs, clustering coefficient, complex networks, directed networks, edges, embeddedness, global, graphs, Links, network, nodes, reinforcement, social network analysis, strength of ties, ties, undirected networks, valued networks, vertices, weighted networks.
The importance of allowing ties to decay Are triangles made up by strong ties?
 RSS feed
RSS feed
1. James @ IST drexel | November 30, 2009 at 6:28 pm
James @ IST drexel | November 30, 2009 at 6:28 pm
nice work! That is exactly what I am thinking.
Do you have a JAVA version of the algorithm?
Thanks
2. Tore Opsahl | November 30, 2009 at 7:30 pm
Tore Opsahl | November 30, 2009 at 7:30 pm
No, only got the R implementation. Let me know if you programme it.
3. Tore Opsahl | March 19, 2011 at 5:00 pm
Tore Opsahl | March 19, 2011 at 5:00 pm
NOTE: There are now some C++ functions. So if you run out of memory or analysing large networks, contact me.
4. Manal Rayess | January 4, 2011 at 12:20 pm
Manal Rayess | January 4, 2011 at 12:20 pm
Hi Tore,
I have a directed NW and clutering_w is giving me 0. As I understood from your paper, you included transitivity in this extended generalized metric.
Any suggestions?
5. Tore Opsahl | January 4, 2011 at 12:36 pm
Tore Opsahl | January 4, 2011 at 12:36 pm
Manal,
The clustering measure varies from 0 to 1. In a directed network, this simply imples that no two-path is closed by a third tie from the first to the third node on the path.
Best,
Tore
6. cookies | June 15, 2011 at 9:43 am
cookies | June 15, 2011 at 9:43 am
Hi Tore,
I want to use this method to evaluate clustering quality, I mean I would like to know the quality of clustering results, is it appropriate?
7. Tore Opsahl | June 16, 2011 at 10:06 pm
Tore Opsahl | June 16, 2011 at 10:06 pm
Hi,
It is meant to test the level of clustering in a network. Have a look at Newman and Girvan’s paper where they propose the edge betweenness method, and defined a quality measure, Q. Also you can look at Krackhardt’s work on ties inside versus ties outside.
Best,
Tore