Defining Two-mode Networks

Network with two types of nodes
One of the first two-mode datasets to be analysed was the Davis’ Southern Women dataset (Davis et al., 1941), which recorded the attendance of a group of women (primary node set) to a series of events (secondary node set). A woman would be linked to an event if she attended it. Another category of two-mode networks that has become popular in recent years is scientific collaboration networks (Newman, 2001). The two sets of nodes are scientists and papers, and a scientist is linked to a paper if she or he is listed as an author. As scientists generally decide whether or not they would like to work on a paper, they are often assumed to be the primary nodes. However, it is not always obvious which node set is the primary one, and in these cases, the research question guides the choice. For example, in the case of interlocking directorates where the two node sets are directors and corporate boards, and ties represent affiliation of directors with boards, it is not clear whether directors or boards are the primary node set (e.g., Levine, 1979; Mizruchi, 1996; Seierstad and Opsahl, 2011). This is likely to be due to tie formation being a mutual process where the directors must (1) be invited to join the board, and (2) accept the invitation.
Analyse as one-mode networks?
Two-mode networks are rarely analysed without transforming them. This is because most network measures are solely defined for one-mode networks, and only a few of them have been redefined for two-mode networks (Borgatti and Everett, 1997; Latapy et al., 2008). Transforming a two-mode network to a one-mode network is often done using a method known as projection. This method operates by selecting one of the two node sets (often the primary node set) and linking nodes from that set if they were connected to at least one common node in the other set. Although the two-mode structure is discarded in this process, it is possible to define tie weights based on it. Specifically, the tie weights are often defined as the number of common nodes. This method was extended by Newman (2001) who argued that tie weights among authors in scientific collaboration networks should be discounted if the authors collaborated on papers with many others. For more information, see the page on projection.
The projection of two-mode networks creates a number of issues. First, each tie in a prototypical one-mode network is assumed to be created separately; however, this is not the case in projected two-mode networks. For example, while a standard phone call creates a communication tie from one person to another, a director forms ties with all the other directors on a board when she or he joins that board. This has direct implications for frameworks that utilize random networks to detect a baseline level (e.g., Opsahl et al., 2008) and when comparing measures observed in a network with those found in corresponding random networks. This is due to the fact that ties in classical random networks are assumed to be independent of each other (Erdos and Rényi, 1959). Although this is neither the case in prototypical one-mode nor projected two-mode networks, the random networks are less comparable to projected two-mode networks than to prototypical one-mode networks as multiple ties can be created due to a single event in these networks. Second, depending on the degree distribution of the non-projected node set, a projected two-mode network tends to have more and larger fully-connected cliques than prototypical one-mode networks (Wasserman and Faust, 1994). These are produced when three or more nodes are connected to a common node in the two-mode network (e.g., all the directors on a single board are connected and form a fully connected clique). This feature impacts a number of network measures, especially those based on triangles including the structural holes measures (Burt, 1992, 2005) and the clustering coefficients (for a review, see Opsahl and Panzarasa, 2009). To exemplify the cliques, and the many triangles, produced when projecting a two-mode network, the figure below shows the main component of the interpersonal network among Norwegian directors.

The network structure among directors (circles) who form part of the largest group of interconnected directors. Two directors are connected if they are members of the same board. The solid circles refer to women, whereas the hollow circles refer to men (Seierstad and Opsahl, 2011).
Weighted Two-mode Networks
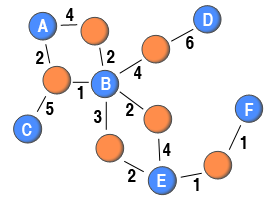
Weighted two-mode network
An example of such a network is online forums where users (node set 1) can post multiple messages to topics or threads (node set 2). Among other measures, there are two ways of operationalising tie weights in these networks. First, it might be the number of messages a user post to a thread. This way wound count the number of interaction in a thread, but be insensitive to the size of messages. As such, a second way of defining tie weights is sum the number of characters in the posted messages. While including the size of messages, this method fails to incorporate the back-and-forth of content. Nevertheless, by include tie weights, the analysis of an online forum might be more accurate than simply ignoring them.
References
Borgatti, S. P., Everett, M. G., 1997. Network analysis of 2-mode data. Social networks 19, 243-269.
Burt, R.S., 1992. Structural holes. Harvard University Press, Cambridge, MA.
Burt, R.S., 2005. Brokerage and closure: An introduction to social capital. Oxford University Press, Oxford, UK.
Davis, A., Gardner, B. B., Gardner, M. R., 1941. Deep South. University of Chicago Press, Chicago, IL.
Erdos, P., Rényi, A., 1959. On random graphs. Publicationes Mathematicae 6, 290-297.
Latapy, M., Magnien, C., Del Vecchio, N., 2008. Basic notions for the analysis of large two-mode networks. Social Networks 30(1), 31-48.
Levine, J., 1979. Joint-space analysis of “pick-any” data: Analysis of choices from an unconstrained set of alternatives. Psychometrika 44(1), 85-92.
Mizruchi, M. S., 1996. What Do Interlocks Do? An Analysis, Critique, and Assessment of Research on Interlocking Directorates. Annual Review of Sociology 22, 271-298.
Newman, M. E. J., 2001. Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Physical Review E 64, 016132.
Opsahl, T., 2013. Triadic closure in two-mode networks: Redefining the global and local clustering coefficients. Social Networks 35, doi:10.1016/j.socnet.2011.07.001.
Opsahl, T., Colizza, V., Panzarasa, P., Ramasco, J.J., 2008. Prominence and control: The weighted rich-club effect. Physical Review Letters 101, 168702.
Opsahl, T., Panzarasa, P., 2009. Clustering in weighted networks. Social networks 31, 155-163.
Seierstad, C., Opsahl, T., 2011. For the few, not the many? The effects of affirmative action on presence, prominence, and social capital of women directors in Norway. Scandinavian Journal of Management 27 (1), 44-54.
Wasserman, S., Faust, K., 1994. Social Network Analysis: Methods and Applications. Cambridge University Press, New York, NY.
Trackback this post | Subscribe to the comments via RSS Feed