Tore Opsahl

Two-mode networks

Many network dataset are by definition two-mode networks (also known as affiliation or bipartite networks). These are a particular type of networks with two sets of nodes and ties are only established between nodes belonging to different sets. This diagram illustrates a binary two-mode network where the colour represent the node set to which a node belongs. One of the first two-mode datasets to be analysed was the Davis Southern Club Women dataset (Davis et al., 1941), which recorded the attendance of a group of women (node set 1) to a series of events (set 2). A woman would be linked to an event if she attended it. Another type of two-mode dataset that has become popular in recent years is scientific collaboration networks. In this type of networks, a tie is established between a scientist (node set 1) and a paper (node set 2) if the scientist authored that paper (e.g., Newman, 2001). Read more…

The ties in two-mode networks can also be differentiated by weights. In these cases, the network would be a weighted two-mode network. An example of such a network is online forums where users (node set 1) can post multiple messages to topics or threads (node set 2). Similarly to weighted one-mode networks, ties can be incorporated in measures. This section mainly deals with binary two-mode networks, but when implemented, the documentation will also include information on weighted two-mode networks.

Projection

Transforming a two-mode network into a one-mode network is often referred to as projection. Although it is preferable to analyse networks in their original form, few methods exist for analysing two-mode networks. As such, projection is the only way to analyse these networks. The process works by selecting one set of nodes, and linking two nodes if they are connected to the same node of the other set. Traditionally, ties in the one-mode networks are without weights. However, it is possible to maintain some of the richness contained within the two-mode structure by carefully considering multiple ways of projecting two-mode networks onto weighted one-mode networks. This enables researchers to conduct a deeper analysis than if the two-mode structure was completely ignored. In fact, the accuracy of metrics might improve substantially (e.g., shortest path calculations). Read more…

Shortest Paths

Shortest paths have variously been calculated in two-mode networks. This page reviews two methods, and suggests how to extend them to incorporate more information in an effort to increase the accuracy of the measures. Specifically, it takes another look at the use of (n+p)x(n+p)-matrices and binary projection methods. While these two methods are computationally fairly different, the outcome is substantially similar. A key limitation of these methods is the exclusion of tie weights. For example, the tie strength between two authors in scientific collaboration is the same irrespectively of the number of co-authored papers. As such, the page goes on to suggest a new method that do incorporate these differences and shows that tie weights can be incorporated, even in binary two-mode networks, to identify the shortest paths and calculate their length. Read more…

Node centrality

Identifying the central nodes in a network has been a major focus of network scholars: Who are the most influential people on Twitter? Which airport is the most important (hint: it’s not Anchorage)? Who is the best connected scientist in a collaboration network (Newman, 2001)? While the first two questions can be answered with node centrality measures for one-mode networks, the third question is related to two-mode networks. In these networks, it is possible to take into consideration the two-mode structure as well as the one-mode structure. This page highlights how degree, closeness, and betweenness can be calculated in two-mode networks. Read more…

Clustering

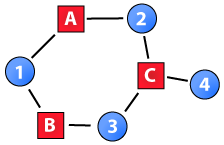Clustering or group formation in networks has been a key topic in social network analysis. A major issue when calculating one-mode clustering metrics on projected two-mode networks is the large number of cliques found in these networks. Specifically, the clustering metrics often overestimates the level of clustering in networks. The overall or global level of clustering in networks is related to the skewness of the secondary nodes’ degree distribution, and the local clustering coefficient is inversely related to nodes’ two-mode degree. This page highlights these issues in detail as well as three clustering metrics specifically designed for two-mode networks. The first measure is a reinforcement metric based on 3-paths and 4-cycles (Robins and Alexander, 2004). The last two are the two-mode global and local clustering coefficients which are based on 6-paths (Opsahl, 2012). Read more…

Structural Holes

Structural holes-measures are based on the local network surrounding focal nodes (Burt, 1992). As such, it is similar to the local clustering coefficient that measures the proportion of ties among contacts that are present. Given the emphasis on ties among contacts, the structural holes measures also suffers from a number of issues when applied to projected two-mode networks. Although the scores are not directly the inverse of nodes’ two-mode degree, they are inversely related (Opsahl, 2012). This page highlights the constraint metric. Read more…

Weighted Rich-club Effect

The weighted rich-club effect tests whether prominent nodes have a tendency of directing their strongest ties towards each other (Opsahl et al., 2008). A key element of the rich-club framework is the use of random networks to detect the baseline level in networks, and then seeing how the observed score deviates from the baseline. In the original paper, only randomisation procedures for one-mode networks were used. This page shows how results are changed when using random two-mode networks. Read more…

Random Two-mode Networks

Random networks is a tool for analysing observed networks. By comparing descriptive metrics of an observed network to ones computed on similar or corresponding random networks, it is possible gauge whether the effects exist and their size as well as whether they are statistically significant. It is important to ensure that the random networks are comparable to the observed network when using random networks as benchmarks. For example, when analysing a projected two-mode network, this is fairly imperative to use projections of random two-mode networks as one-mode random networks are based on one-mode assumptions (e.g., each tie can be formed independently; however multiple ties can be formed in a projection when one tie is formed in the two-mode network). Read more…

References

Burt, R. S., 1992. Structural Holes: The Social Structure of Competition. Harvard University Press, Cambridge, MA.

Davis, A., Gardner, B. B., Gardner, M. R., 1941. Deep South. University of Chicago Press, Chicago, IL.

Newman, M. E. J., 2001. Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Physical Review E 64, 016132.

Opsahl, T., 2013. Triadic closure in two-mode networks: Redefining the global and local clustering coefficients. Social Networks 35, doi:10.1016/j.socnet.2011.07.001.

Opsahl, T., Colizza, V., Panzarasa, P., Ramasco, J. J., 2008. Prominence and control: The weighted rich-club effect. Physical Review Letters 101 (168702). arXiv:0804.0417.

Robins, G., Alexander, M., 2004. Small worlds among interlocking Directors: Network structure and distance in bipartite graphs. Computational and Mathematical Organization Theory 10 (1), 69–94.