Tore Opsahl

Thesis: 4.3 Longitudinal binary networks

We propose to use a model that is based on the conditional logistic regression framework (Breslow, 1996; Cox and Hinkley, 1974; Hosmer and Lemeshow, 2000) or discrete choice modelling (McFadden, 1973) to investigate growth mechanisms in the network evolution. This is a particular type of statistical model that tests whether chosen options or cases have certain properties that a set of other options or cases do not have. For example, suppose that a number of people can choose their mode of transportation to work. For each option that a person can choose, there are a set of known parameters specific to that option. This could include duration, cost, inconvenience, energy consumption, and comfort among others. In addition, for each person, the chosen option is known. Then, a conditional logistic regression could be used to probe which parameters, and the extent to which they guide the choice that a person makes.

This model can also be used to study other decision processes. In fact, we can apply this model to investigate why nodes form \textit{new} ties with certain other nodes (i.e., binary ties). The components of this model are as follows. At a given time t, a node i decides to form a tie. This tie can be directed towards the set of available nodes in the network at that time . Since we are studying a binary network, we assume that this set includes all the nodes in the network at time t that node i is currently not tied to. The node that receives the tie, node j, can have a number of properties, . These properties might include terms related the mechanisms outlined above, such as the in-degree of node j (preferential attachment) and whether node j has already formed a tie with node i (reciprocity). The purpose of the conditional logistic regression model is to see whether the properties of node j, , stand out from the properties of all the available nodes, . We choose to use the properties observed before the tie is created () as we seek to understand why node j was the one that was selected by node i. We formalise the model as follows:

where is a vector of coefficients. The coefficients that best fit the data are found by maximising the log of the equation (Hosmer and Lemeshow, 2000).

This model is analogous with other models that have been suggested in the literature. First, Snijders (2001) defined a model similar to the above model when proposing the SIENA model. Although the data used in the SIENA model is multiple snapshots of the network structure, the model is defined for network data where the exact sequence of ties is known, and estimation is used for the panel data. Second, Butts (2008) suggested a hazard or survival model for studying the network evolution. This model was applied to the radio communication data collection on the World Trade Center disaster. However, unlike Butts’ model, the model above is concerned with directed one-mode networks, in which the aim is to detect preferences of nodes in how they direct ties toward other.

The conditional logistic regression model suffers from a number of limitations. A major one is that each tie can be directed towards many possible nodes (i.e., the set $A_t$ is large). This implies that the ratio been the realised option or the observed tie (dependent variable equal to 1) and all the others (dependent variable equal to 0) is very small. In fact, most conditional logistic regressions in epidemiological studies have a ratio between 1:1 and 1:5 (Hosmer and Lemeshow, 2000). A lower ratio could create a number of issues for estimation of the coefficients (King and Zeng, 2001). In particular, the logistic regression models can greatly underestimate the probability of events when the ratio is very small.

For the online social network the ratio is extremely small. A user can choose to direct a tie to one of the 1,898 other users when all users are included in the network. Thus, the ratio can be as small as 1:1897. Moreover, the number of observations in the regression would be extremely large. Again, in the case of the online social network with 20,296 binary directed ties, the size of the sample would be approximately 24 million observation (or 38.5 million observations if all nodes are considered available from ). A common method to overcome these two limitations is to use a matched sample (Hosmer and Lemeshow, 2000; Powell et al., 2005). To this end, for each realised case, a number of other observations are picked as control cases. This method can also be applied to our proposed use of the conditional logistic regression framework. For each tie that is formed, a number of control nodes are selected. These should be randomly selected from the available nodes in the network. A sensitivity analysis of the number of control cases is conducted in Section 4.5. Unless otherwise specified, in the remaining of this chapter, for each observed tie we include 19 control cases. Thus, the sample includes 20 observations for each observed tie. The analysis was repeated multiple times with different sets of control nodes and results were consistent. In addition to making the sample balanced for each tie, this also ensures that the method can scale to large datasets.

We now consider a number of network growth mechanisms in an effort to understand how new ties were formed in the online social network (Panzarasa et al., 2009). Although, it can be reasonably argued that most networks develop over time, this is the only network available to us where the exact sequence of ties is known. Therefore, we can only apply the method within this Chapter to this network and not the other networks presented in Section 1.4. For example, in Chapter 2 the clustering coefficient revealed an above random likelihood of a generating a tie between two nodes that share a common contact in the network. In what follows, we first test a number of mechanisms independently, and then together, within the conditional logistic regression framework.

First, as mentioned above, the network was found to exhibit a high number of triangles as a clustering coefficient of 0.0568 was obtained for the undirected network (Eq. 2 in Chapter 2). This is over 7 times larger than what we would expect in a corresponding classical random network (Erdos and Renyi, 1960). Based on this finding, we hypothesise that the likelihood of a tie from one person to another increases as a function of the number of common friends the two people share. In particular, we define as the number of nodes that 1) node i is already tied to, and 2) are already tied to node h (see Figure 12 for a schematic representation).

We found support for this hypothesis. The coefficient that yielded the highest maximum log-likelihood was 0.233 with a standard error of 0.0389 (). This means that people in the online community are more likely to create a tie to others with whom their existing contacts are already tied to. More specifically, given two users, for each additional common contact they share, the likelihood of a tie between them increases by 26% ( equals an odds ratio of 1.26).

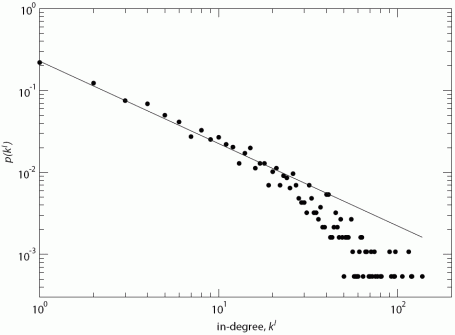
Second, the ties are not homogeneously distributed across the nodes in the online community (Panzarasa et al., 2009). While the majority of nodes in the network is connected to few others, there is a subset of extremely well-connected nodes. More specifically, the in-degree distribution follows a power-law function, , with an exponent of less that 2 (see the solid line in Figure 13). This suggests that the network is "scale-free" (Barabasi et al., 2002). This distribution has been replicated in growing random networks where nodes that already have received relatively many ties have a higher probability of attracting new ties than nodes with fewer ties (Barabasi et al., 2002; Dorogovtsev and Mendes, 2003; Jeong et al., 2003). Thus, it has been speculated that a "popularity is attractive"-mechanism is the cause of the observed distribution. Since we found a scale-free distribution for the online social network, we hypothesise that users in the online community were attracted to other users that were "popular". More specifically, we define as the number of nodes that are already tied to node h before a possible tie is created at t. We found support for this hypothesis as a coefficient of 0.037 was obtained with a standard error of 0.0006 (). For each additional tie that terminates at a node, the likelihood that a node will receive a new tie increases with 3.7%.

Third, 12,916 of the 20,296 directed ties in the online community occurred within a dyad with another tie (reciprocated). In a classical random network the number of reciprocated ties is likely to be much smaller. More specifically, since each directed tie is independent of all the other ties, the probability of a tie being reciprocated is equal to the probability of a tie (Erdos and Renyi, 1960; Rapaport, 1953). For the online social network, the probability of a directed tie is 0.0056. Thus, the expected number of reciprocated ties is 114. Based on the large difference between the observed and expected number of reciprocated ties, we hypothesise that reciprocity exerted a strong effect on the evolution of the network. was defined as 1 if node h had already directed a tie towards node i, and 0 otherwise. We found support for this hypothesis as a coefficient of 4.85 was obtained with a standard error of 0.105 (). This implies that reciprocated ties are 128 times more likely to be formed than non-reciprocated ties.

Fourth, we focus on homophily, namely the tendency of similar nodes to create ties among themselves (Lazarsfeld and Merton, 1954; Louch, 2000; McPherson et al., 2001). This mechanism has been found to be responsible for the creation of tightly knit groups of similar individuals in a social network (Kossinets and Watts, 2006). This might be due to similar background (Hallinan and Kubitschek, 1988; Lazarsfeld and Merton, 1954; McPherson et al., 2001). Drawing on these empirical studies, we hypothesise that the likelihood of a tie between two people increases as a function of their social similarity. When students registered for the online community, they supplied a number of demographic characteristics or attributes, v. These included the individuals’ gender, age, year of study, region of origin, and marital status. For each ordinal attribute (i.e., age and year of study), we constructed a similarity index. This index was defined the ()-dyad as 1 minus the standardised absolute difference between and . This formula is also used by Siena (Snijders, 2001): . For the other nominal attributes, we constructed a dummy term indicating whether the two nodes had the same value, e.g., set to 1 if two nodes have the same gender and 0 otherwise. By testing these terms independently, we found that the coefficients for all attributes, excluding gender, were positive and significant (see Models 4-7 in Table 6). Conversely, having the same gender significantly decreased the likelihood of creating a tie (see Model 8). This implies that a male (female) user was more likely to communicate with a female (male) one than with another male (female) user.

Finally, we tested the effects of focus constraints on network evolution. This mechanism is responsible for the increase of the likelihood that institutionally or geographically bounded nodes form ties among themselves (Feld, 1981; Monge et al., 1985). As triadic closure and homophily, this mechanism is therefore responsible for the generation of groups of well-connected nodes. When students registered on the web site of the community, in addition to the demographic attributes, they also supplied information about the course they attended. Based on this information, we hypothesise that two students belonging to the same school have a larger likelihood of creating a tie than two students from different schools. We found support for this hypothesis as a coefficient of 0.278 was obtained with a standard error of 0.028 (). This implies that belonging to the same school increases the likelihood of forming a tie with 32%.

A limitation of the analysis we conducted so far lies in the fact that it focuses on a single mechanism in turn. However, networks are likely to evolve as a result of a combination of mechanisms (Snijders, 2001; Wasserman and Pattison, 1996). This limitation can be easily overcome since we are using a regression framework which allows for multiple independent variables (Cox and Hinkley, 1974; Hosmer and Lemeshow, 2000). Thus, we can to assess the likelihood of a new tie as a function of two or more terms.

Model 10 in Table 6 shows the coefficients and significance of all the terms previously tested independently when tested together. A number of observations are in order. First, the two terms with the highest absolute z-scores (i.e., the coefficient divided by the standard error) are network effects, namely reciprocity () and in-degree (). This signals the importance of path dependency in the evolution of the network.

Second, the two terms similar age and triadic closure lost their significance. These were also the terms with the lowest absolute z-score in the independent tests. A possible reason for the loss of significance is multicollinearity. If two terms are representing the same underlying factor in the data, the maximum likelihood estimation would not be able to determine which of the two terms is responsible for the increase in likelihood of a tie. This might be the root of the non-significance of both these terms. Conceptually, there is a link between the age of a person and the year of study as most people in the US join university when they leave school at the age of 18. In fact, between similar age and similar year of study the pair-wise correlation coefficient is 0.2649, whereas between similar age and all other terms the coefficients are less than 0.1. The results in Table 6 might indicate that it is not age of people that determines whether ties are formed, but the advancement in their university education.

The triadic closure term is associated with the term indegree. Given an equal number of triplets originating from the creator of a tie, the higher the in-degree of a target node, the more triplets are likely to terminate at that node. Therefore, the term triadic closure should be correlated with the term indegree. In fact, the pair-wise correlation coefficient between triadic closure and indegree terms is 0.2998, whereas the coefficients between triadic closure and all other terms are less than 0.1. Thus, the positive effect of triadic closure in the independent test might be a reflection of the correlation with indegree. It is rare to find a social network without a triadic closure effect. However, this network is a special kind of social network where a person communicates individually with his or hers contacts and never in a group. Therefore, the contacts of a person cannot be observed by each other, and they might not be aware of each other.

Third, the size of the in-degree effect is reduced when other mechanisms are included. Unlike an increase of 3.7%, when combined with other measures, each additional in-degree only increases the likelihood of receiving a tie by 2.9%. This result should be assessed in the light of the controversal debate between two camps within the social networks community. On the one hand, there are scholars, especially statistical physicists, that tend to argue in favour of the ubiquity of preferential attachment as a growth mechanism that explains how a variety of real-world networks evolve (Barabasi et al., 2002; Dorogovtsev and Mendes, 2003). On the other, it is argued, especially by social scientists, that preferential attachment is inaccurately measured (Borgatti et al., 2006) or that other forces are at work in driving network evolution, such as homophily and triadic closure (Powell et al., 2005; Kossinets and Watts, 2006). Our results indicate that these arguments are not mutually exclusive and together they may well suggest that the evolution of the network is governed by the contribution of multiple mechanisms.