Tore Opsahl

Thesis: 4.4 Longitudinal weighted networks

An aspect of social networks that is often overlooked is the weight of ties as most empirical studies are in fact based on binary network datasets, and therefore give no indication about the role of ties of different strength in shaping the structure and function of the network (see Section 1.1). However, strong and weak ties are associated with different properties, and it is therefore important to distinguish between them. For example, strong ties have been associated with trust and transfer of tacit knowledge (Reagans and McEvily, 2003; Levin and Cross, 2004; Uzzi and Spiro, 2005), whereas weak ties have been linked with access to novel explicit knowledge (Burt, 1992; Granovetter, 1973).

The ERG and SIENA models currently cannot be applied to weighted networks (an extension has been proposed by Snijders and Steglich, 2008). Conversely, the model proposed in this Chapter can easily be extended to weighted networks by relaxing some of its assumptions. In weighted networks, multiple ties can exists from one node to another. This means that a tie is not only formed when a node interact with another for the first time, but every time an interaction occurs. Multiple ties reinforce the tie already existing from the creating node to the target node. Therefore, in a weighted network, we assume that includes all other nodes in the network when a tie is created, even those that the creator of the tie is already connected to.

Moreover, in weighted networks additional mechanisms might be responsible for tie generation. In the online community, an average user has sent 31.5 messages to 10.7 people. This means that two-thirds of messages were used to reinforce existing ties. Since the network is sparse and on average ties have been reinforced roughly two times, we hypothesise that reinforcement is likely to affect the likelihood of a future tie. In other words, we believe that a new tie is more likely to occur between two nodes that are already connected than between nodes that are disconnected. We found support for this hypothesis as we obtained a positive and significant coefficient of 0.7598 with a standard error of 0.0759 ($p<0.001$). This coefficient translates into an odds ratio of 2.14 (), which suggests that each previous message sent between two nodes roughly doubles the likelihood of another message being sent.

However, this result is obtained by testing reinforcement independently without taking into account the other mechanisms that proved to be significant for the evolution of the binary network. Thus, the next step is to include multiple effects in our assessment of weighted networks. Model 2 in Table 7 shows reinforcement modelled together with the terms used in the binary analysis. Even though in this case we found a smaller coefficient for reinforcement, the coefficient remained positive and extremely significant ().

All of the terms that were previously used in the analysis of network evolution were designed for binary networks. However, some of them can be generalised to weighted networks. As shown in Chapter 2, a triplet value can be used to differentiate triplets. We proposed four methods for determining the triplet value. It can be the arithmetic mean, geometric mean, the maximum, or the minimum of the two weights that compose the triplet. Building on Opsahl and Panzarasa (2009), Snijders and Steglich (2008) used the concept of a triplet value to model triadic closure in a proposed extension of the SIENA model to weighted networks. They used the minimum and geometric mean methods for defining the triplet value and for the ()-dyad summed the values of the triplets that originate at node i and terminate at node h. These terms can be formalised as follows:

where i is the creating node and h is the target node of a possible tie, and k represents any other node that i is tied to.

To illustrate these two effects, Figure 14 exemplifies a possible directed tie between node i and h (dashed line). Node i is tied to three other nodes , and . The first two of these nodes are tied to the target node h. The two terms would be equal to 5 and 6.29, respectively, for this tie. The calculations are: and for the two methods, respectively.

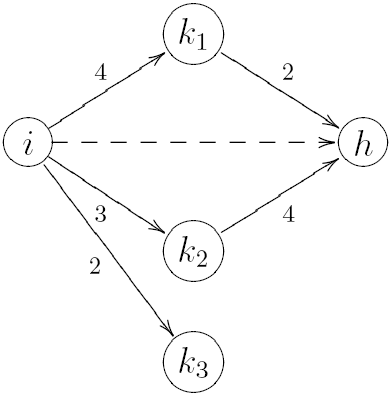
Figure 14: Example of weighted triplets that originate at node i and terminate at target node h of a possible tie.

Following our results for the binary network, we first hypothesise that the two terms, formalised in Equations 12a and b, increase the likelihood of a tie. In addition, we hypothesise that if the two generalised terms replace the simpler binary term (the number of common friends; the term triadic closure as defined in the previous section) the models produce a higher Wald due to the finding in Chapter 2 that strong ties are more likely than weak ties to be part of closed triplets in the online social network (see Section 2.3). As shown by Models 3 and 4 in Table 7, we found only partial support for the first hypothesis. We chose not to test the three triadic closure terms together due to high correlation. This correlation is not surprising since the three terms are operationalisations of the same mechanism. Moreover, Models 3 and 4 had a lower Wald than Model 2. Therefore, we did not find support in favour of our second hypothesis that the generalised triadic closure terms were better than the binary term.

Furthermore, for weighted networks in-degree is often redefined as node in-strength (see Chapter 3, and Barrat et al., 2004; Newman, 2004a; Opsahl et al., 2008). A node’s in-strength is the sum of the weights attached to the ties that terminate at the node. This is equal to the in-degree of a node if all ties carries a weight of 1, i.e. if the network is binary. Therefore, this term can only be included in an assessment of weighted networks. In the light of the improvement of results in Chapter 3 when out-strength replaced out-degree, here we hypothesise that a similar improvement of results is likely to occur when in-strength is used instead of in-degree. However, as shown by Model 5 in Table 7, we did not find support for this hypothesis. In fact, a lower overall Wald was found when in-degree was replaced with in-strength. A possible explanation for this is that it is not the total number of messages received, but the number of unique contacts that most accurately gives an indication of a user’s popularity.

Finally, the results from the analysis of the binary network are consistent with what was found for the weighted network. First, the two terms with the highest absolute z-scores are still network effects: reinforcement and reciprocity. Second, the term similar age remains not significant, while the term triadic closure is just within the level. This suggests that people's age is indeed not a relevant predictor of ties, and triadic closure does not have a strong statistically significant effect on network growth. Third, the magnitude of the in-degree effect is further mitigated in the analysis of the weighted network. In Model 2 of Table 7, the increase in likelihood of receiving a tie only increases of 2.15% for each additional in-degree of a node. This suggests that the explanatory power of preferential attachment as a mechanism for network dynamics is mitigated when a broader prespective is adopted that takes into account not only the reinforcement mechanism, but also the weight of ties and ties used to reinforce.