Tore Opsahl

Thesis: 3.3 Empirical tests

We apply the above framework to three of the real-world networks described in Chapter 1. The networks are: the US airport network, the scientific collaboration network (Newman, 2001b,c), and the the online social network. We choose these networks due to their size. The remaining social networks had less than 100 nodes. We deem these networks too small.

3.3.1 Club of the most connected nodes

In analogy with the topological rich-club coefficient, we begin by defining the prominence parameter r as the degree of nodes. In so doing, we assess whether there is a tendency of highly connected nodes to forge stronger ties among one another than would be the case if weights were randomly attached to ties. We use the Weight reshuffle null model, since it is the simplest null model that preserves the prominence of nodes, i.e. their degree. We also consider the Weight & Tie reshuffle null model to show how an increased level of randomness affects the results.

Figure 7 reports the weighted and topological (inset) rich-club ratios for the three networks. The diagrams on the left show results based on the Weight reshuffle null model, whereas the ones on the right show results based on the Weight & Tie reshuffle null model (The Directed Weight reshuffle null model also maintains the degree distribution of the observed network. However, a random networks created using this null model is less different from the observed network than random networks created using the other two null models. In particular, if a node is only connected to one other node, the tie cannot be randomised. Nevertheless, similar results are found when this null model is used (see Appendix B.1).). The airport network shows a positive weighted rich-club ordering, as can be identified from the remarkable growth of both when the subsets of high degree nodes become increasingly restrictive. Moreover, a mild topological effect is found. This is in agreement with previous studies that found correlations between weight of the ties and degrees of the nodes (Barrat et al., 2004; Guimera et al., 2005; Wu et al., 2006). Routes among hub airports, with flights to many destinations, are the busiest ones in the U.S.

Conversely, while the scientific collaboration network has a strong positive topological rich-club effect, it does not exhibit any weighted rich-club ordering. This suggests that the authors who collaborate with many others tend to collaborate among themselves. However, their collaborations are not stronger than randomly expected. As shown in the second row of Figure 7, the coefficient for the observed network is close to the value found in the random network: remains flat around 1 for a large range of values of k. A substantial departure of the coefficient from the expected value is found only for very high values of k, where only 29 authors are classified as prominent. However, at this level, the observed coefficient does not depart from the random one in a statistical significant way. These results are in agreement with previous studies that showed that the strong ties in collaboration networks tend to be independent of the degrees of the nodes (Ramasco and Goncalves, 2007; Ramasco, 2007).

Finally, the topological and weighted rich-club coefficients display strikingly different trends from each other for the online social network. While the topological coefficient decreases with k and remains below 1 throughout the whole range of degrees, the weighted coefficient shows a mild increasing trend. Very gregarious individuals, namely the ones that contact a large number of other users, poorly communicate with one another. However, when they do, they choose to forge ties that are stronger than randomly expected. When there are few nodes left in the network (), the coefficient fluctuates. Moreover, the observed coefficient does not significantly deviate from the random one in this range of k.

The limitations of defining prominence in terms of degree and the advantages of considering other ordering properties are illustrated by using the example of the scientific collaboration network. In this network, each paper is translated into a fully connected group of collaborators (or cliques). Therefore, the whole network can be represented as a set of cliques that overlap when authors write papers with different others. When a paper is co-written by a large number of authors, these authors take on a high degree and thus increase their chances to become classified as prominent. However, due to the operationalisation of tie strength, the weight of these ties are weak (Newman, 2001c). For example, if 101 authors write only a single paper together, they would all receive a degree of 100, but the ties among them would only have a weight of 0.01. Thus, large collaborations tend to secure the prominent status for the authors, yet generate weaker ties among the prominent nodes than smaller collaborations.

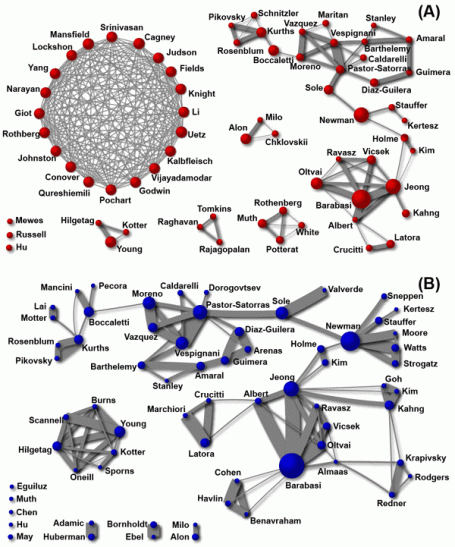
To illustrate this issue, we focus on a subset of the scientific collaboration network that includes only authors working on network theory and experiments (network science network; Newman, 2006). This network displays similar weighted and topological rich-club effects as the observed overall network (see Appendix B.2). Experimental papers on biological networks are written by a large number of authors, and therefore only one of these papers may suffice to substantially increase the topological rich-club ordering. Figure 8a and b show all nodes with and , respectively, and the ties among them, in the network science network. The large clique in Figure 8a consists of 20 authors that are tied together by a single paper (Uetz et al., 2000). Only 3 of these authors are also tied together by an additional paper. The ties among the other 17 authors who only collaborated on the single publication have a weight of 0.05263, which is the minimum tie weight in the network. Therefore, the existence of large collaborations increases the number of weak ties in the numerator of the coefficient, which reduces the weighted rich-club effect. This can offset a possible weighted rich-club effect among the other prominent nodes. Therefore, another ordering property that does not classify the authors of a single large collaboration as prominent is needed. As can be seen in Figure 8b, if prominence is based on the strength of the nodes (which is the number of co-authored papers published by authors), the subset of nodes and, more importantly, the weight of the ties among them, change substantially.

3.3.2 Club of the most active nodes

In light of this observation, the next step is thus to define prominence r in terms of node strength. In so doing, we shift our attention from the most connected to the most involved nodes in the network activity. The weighted rich-club assessment then measures whether these nodes direct their strongest ties preferentially towards each other. To ensure that the prominent nodes in the null model remain the same as in the observed network, we need to preserve in addition to . Therefore, we adopt the Directed Weight reshuffle null model that also preserves this distribution. It is worth noting that the construction of this null model for the undirected scientific collaboration network is a methodological extension of the original procedure. As suggested in Section 3.2.1, a more appropriate null model might be reshuffling the two-mode structure instead the one-mode projection. However, only the one-mode structure of this network was available to us.

Figure 9 shows a positive weighted rich-club ordering for all the three networks analysed. Highly involved nodes preferentially direct their strongest ties towards one another, and this tendency becomes more pronounced as the number of prominent nodes decreases. The airport network exhibits a strong weighted rich-club effect. This result suggests that traffic is heavier among busy airports than randomly expected. Moreover, it corroborates the result obtained when prominence was defined in terms of k. This finding is not surprising given the previous result as node degree and strength are correlated in this network (Barrat et al., 2004). More generally, if node degree and strength are correlated, the subsets of prominent nodes obtained with the two definitions are likely to be composed of the same nodes. If this is the case, then the results will not differ.

Defining prominence in terms of strength is especially relevant for the scientific collaboration network, where tie strength is equal to the number of co-authored papers published by each author, and can therefore be seen as a measure of productivity. In this case, the weighted rich-club ordering is positive among authors that published many papers, unlike what was found when prominence was defined in terms of number of collaborators. This signals that strength is a better parameter than degree for identifying a subset of nodes with stronger ties among themselves than randomly expected.

The online social network also reveals a pronounced positive weighted rich-club ordering, thus suggesting that active online users tend to communicate frequently with one another. This corroborates the findings when the definition of prominence was based on degree. A possible cause of similar results is correlation between node degree and strength. In fact, in this network, the pair-wise correlation between these two properties is 0.90.

For very high values of s, only few nodes are part of the subsets of prominent nodes in the three networks. This implies a high level of fluctuations in for high values of s. It can be speculated that the drop observed in the social networks may be due to some form of competition among very prominent nodes. This might account for the reluctance of prominent authors to establish strong ties among themselves, as is suggested by the lack of interaction among the three most productive authors in Figure 8B: Barabasi, Newman, and Vespignani.

3.3.3 Club of the nodes with the highest average weight

While node strength gives is a proxy of a node’s involvement in the network activity, it does not distinguish between nodes with a large number of weak ties and nodes with a small number of strong ties, given the same value of node strength. In addition, due to high correlation between node degree and strength in the networks, the two ordering properties are likely produce similar subsets of prominent nodes. To address these issues, we define the prominence parameter r in terms of the average weight (Ramasco and Morris, 2006). A positive coefficient suggests that the nodes with strong ties choose to direct these with each other. We use the Directed Weight reshuffle null model to keep invariant for each node, thus ensuring that the prominence of the nodes in the observed network and in its corresponding randomised version remain the same.

Figure 10 shows the weighted rich-club coefficient for all the three networks. The airport network displays a positive signal which substantially departs from the random baseline only at high values of the average weight. Airports characterised, on average, by very busy routes tend to direct these routes to one another.

Positive signals are also found for the scientific collaboration network and the online social network. In the collaboration network, authors that show the ability to commit themselves to their collaborators tend to forge strong ties among one another. In the online social network, strong bonds link online users that are capable of developing strong relationships.