Node Centrality in Weighted Networks
A star network with 5 nodes and 4 edges. The size of the nodes corresponds to the nodes’ degree. Adapted from Freeman (1978) and Opsahl et al. (2010).
The three measures have been generalised to weighted networks. In a first set of generalisations, Barrat et al. (2004) generalised degree by taking the sum of weights instead of the number ties, while Newman (2001) and Brandes (2001) utilised Dijkstra’s (1959) algorithm of shortest paths for generalising closeness and betweenness to weighted networks, respectiviely (see Shortest Paths in Weighted Networks for details). These generalisations focused solely on tie weights and ignored the original feature of the measures: the number of ties. As such, a second set of generalisation were proposed by Opsahl et al. (2010) that incorporates both the number of ties and the tie weights by using a tuning parameter.
Degree
Degree is the simplest of the node centrality measures by using the local structure around nodes only. In a binary network, the degree is the number of ties a node has. In a directed network, a node may have a different number of outgoing and incoming ties, and therefore, degree is split into out-degree and in-degree, respectively.
Degree has generally been extended to the sum of weights when analysing weighted networks (Barrat et al., 2004; Newman, 2004; Opsahl et al., 2008), and labeled node strength. It is equal to the traditional definition of degree if the network is binary (i.e., each tie has a weight of 1). Conversely, in weighted networks, the outcomes of these two measures are different. Since node strength takes into consideration the weights of ties, this has been the preferred measure for analyzing weighted networks (e.g., Barrat et al., 2004; Opsahl et al., 2008). However, node strength is a blunt measure as it only takes into consideration a node’s total level of involvement in the network, and fail to take into account the main feature of the original measures formalised by Freeman (1978): the number of ties. This limitation is highlighted for degree centrality by the three ego networks from Freeman’s third EIES network. The three nodes have roughly sent the same amount of messages; however, to a quite different number of others. If Freeman’s (1978) original measure was applied, the centrality score of the node in panel A is almost five times as high as the node in panel C attains. However, when using Barrat et al.’s generalisation, they get roughly the same score.
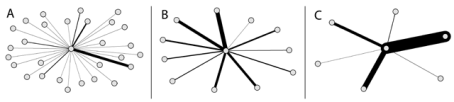
Ego networks of Phipps Arabie (A), John Boyd (B), and Maureen Hallinan (C) from Freeman's third EIES network. The width of a tie corresponds to the number of messages sent from the focal node to their contacts. Adopted from Opsahl et al. (2010).
In an attempt to combine both degree and strength, Opsahl et al. (2010) used a tuning parameter to set the relative importance of the number of ties compared to tie weights. Specifically, the proposed degree centrality measure was the product of the number of nodes that a focal node is connected to, and the average weight to these nodes adjusted by the tuning parameter. There are two benchmark values for the tuning parameter (0 and 1), and if the parameter is set to either of these values, the existing measures are reproduced (Barrat et al., 2004; Freeman, 1978). If the parameter is set to the benchmark value of 0, the outcomes of the measures are solely based on the number of ties, and are equal to the one found when applying Freeman’s (1978) measure to a binary version of a network where all the ties with a weight greater than 0 are set to present. In so doing, the tie weights are completely ignored. Conversely, if the value of the parameter is 1, the measure is based on tie weights only, and are identical to the already proposed generalisation (Barrat et al., 2004). This implies that the number of ties is disregarded. The table below highlights the differences between the degree-measures.
| Node | Degree measure from | |||
|---|---|---|---|---|
| Freeman (1978) | Barrat et al. (2004) | Opsahl et al. (2010; alpha=0.5) | Opsahl et al. (2010; alpha=1.5) | |
| Phipps Arabie (A) | 28 | 155 | 66 | 365 |
| John Boyd (B) | 11 | 188 | 45 | 777 |
| Maureen Hallinan (C) | 6 | 227 | 37 | 1396 |
To calculate the degree scores of nodes, below is a sample code for calculating the degree scores of the neurons of the c.elegans worm (Watts and Strogatz, 1998) using the R-package tnet.
# Load tnet
library(tnet)
# Load the neural network of the c.elegans network
data(tnet)
# Calculate the out-degree of neurons and the generalised measures (alpha=0.5)
degree_w(net=celegans.n306.net, measure=c("degree","output","alpha"), alpha=0.5)
# Calculate the in-degree of neurons and the generalised measures (alpha=0.5)
degree_w(net=celegans.n306.net, measure=c("degree","output","alpha"), alpha=0.5, type="in")
Closeness
Closeness is defined as the inverse of farness, which in turn, is the sum of distances to all other nodes (Freeman, 1978). The intent behind this measure was to identify the nodes which could reach others quickly. A main limitation of closeness is the lack of applicability to networks with disconnected components: two nodes that belong to different components do not have a finite distance between them. Thus, closeness is generally restricted to nodes within the largest component of a network. The blog post Closeness Centrality in Networks with Disconnected Components suggests a method for overcoming this limitation,
Closeness has been generalised to weighted networks by Newman (2001) who used Dijkstra’s (1959) algorithm (see Shortest Paths in Weighted Networks for details). To quickly reiterate Dijkstra’s (1959) and Newman’s (2001) work here:
- Dijkstra (1959) proposed an algorithm to find the shortest paths in a network where the weights could be considered costs. The least costly path connecting two nodes was the shortest path between them (e.g. a network of roads where each leg of road has a time-cost assign to it).
- Newman (2001) transformed the positive weights in a collaboration network into costs by inverting them (dividing 1 by the weight).
- Based on the inverted weights, Newman (2001) applied Dijkstra’s algorithm and found the least-costly paths among all nodes.
- The total cost of the paths from a node to all others was a measure of farness: the higher the number, the more it cost a node to reach all other nodes. To create a closeness measure, Newman (2001) followed Freeman (1978) and inverted the numbers (1 divided by the farness). Thus, a high farness was transformed into a low closeness, and a low farness was transformed into a high closeness.
Similarily to Barrat et al.’s (2004) generalisation of degree, Newman’s (2001) generalised algorithm solely focuses on the sum of tie weights, and fails to consider the number of ties on paths. Opsahl et al. (2010) generalisation of shortest paths can be applied to determining the length of them.
To calculate the closeness scores of nodes, below is a sample code for calculating the closeness scores of the neurons of the c.elegans worm (Watts and Strogatz, 1998) using the R-package tnet.
# Load tnet library(tnet) # Load the neural network of the c.elegans network data(tnet) # Calculate the binary closeness scores closeness_w(net=celegans.n306.net, alpha=0) # Calculate the first generation weighted closeness scores closeness_w(net=celegans.n306.net, alpha=1) # Calculate the second generation weighted closeness scores (alpha=0.5) closeness_w(net=celegans.n306.net, alpha=0.5)
Betweenness
The extent to which a node is part of transactions among other nodes can be studied using Freeman’s (1978) betweenness measure. In the sample network on the right, if the ties did not have a weight assigned to them, the flashing grey lines represent the 9 shortest paths in the network that pass through intermediate nodes. The highlighted node is an intermediate on 8 of these paths. This will give this node a betweenness score of 8.
Brandes (2001) proposed a new algorithm for calculating betweenness faster. In addition to reducing the time, this algorithm also relaxed the assumption that ties had to be either present or absent (i.e. a binary network), and allowed betweenness to be calculated on weighted networks (note that this generalisation is separate from the flow measure proposed by Freeman et al., 1991, which might be more appropriate in certain settings). This generalisation takes into account, that in weighted networks, the transaction between two nodes might be quicker along paths with more intermediate nodes that are strongly connected than paths with fewer weakly-connected intermediate nodes. This is due to the fact that the strongly connected intermediate nodes have, for example, more frequent contact than the weakly connected ones. For example, the tie between the top-left node and the focal node in the sample network above has four times the strength of the tie between the bottom-left node and the focal node. This could mean that top-left node has more frequent contact with the focal node than the bottom-left node has. In turn, this could imply that top-left node might give the focal node a piece of information (or a disease) four times quicker than the bottom-left node. If we are studying the nodes that are most likely to be funnelling information or diseases in a network, then the speed at which it travels, and routes that it takes, are clearly affected by the weights. The identification of the Shortest Paths in Weighted Networks can also be used when identifying the nodes which funnel transactions among other nodes in weighted networks. If we assume that transactions in a weighted network follow the shortest paths identified by Dijkstra’s algorithm instead of the one with the least number of intermediate nodes, then the number of shortest paths that pass through a node might change.
| Node | Betweenness measure from | ||
|---|---|---|---|
| Freeman (1978) | Brandes (2001) | Opsahl et al. (2010; alpha=0.5) | |
| 1 | 0 | 4 | 0 |
| 2 | 8 | 8 | 8 |
| 3 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 |
| 5 | 4 | 4 | 4 |
| 6 | 0 | 0 | 0 |
Now, node 1 (A) has gotten betweenness score of 4 as well. This is because the indirect path from node B to node C through A is used instead of the direct connection.
Similarily to Newman’s (2001) generalisation of closeness, Brandes’ (2001) generalised algorithm solely focuses on the sum of tie weights, and fails to consider the number of ties on paths. Opsahl et al. (2010) generalisation of shortest paths can also applied to identifying them.
To calculate the betweenness scores of nodes, below is a sample code for producing the three tables above using the R-package tnet.
# Manually enter the example network net <- cbind( i=c(1,1,2,2,2,2,3,3,4,5,5,6), j=c(2,3,1,3,4,5,1,2,2,2,6,5), w=c(4,2,4,1,4,2,2,1,4,2,1,1)) # Calculate the binary betweenness measure betweenness_w(net, alpha=0) # Calculate the first generation weighted betweenness measure betweenness_w(net, alpha=1) # Calculate the first generation weighted betweenness measure betweenness_w(net, alpha=0.5)
Note: The implementation of Brandes’ (2001) algorithm finds multiple paths if they have exactly the same distance. For example, if one path is found over the direct tie with a weight of 1 (distance = 1/1 = 1) and a second path is through an intermediary node with two ties with weights of 2 (distance = 1/2 + 1/2 = 1), the two paths have exactly the same distance. However, if there is a third path through two intermediaries with three ties with weights of 3 (distance = 1/3 + 1/3 + 1/3), it does not exactly equal 1 as computers read these values as 0.3333333 and the sum of these values is 0.9999999. Therefore, this path is considered shorter than the other two paths (distance = 1).
References
Barrat, A., Barthelemy, M., Pastor-Satorras, R., Vespignani, A., 2004. The architecture of complex weighted networks. Proceedings of the National Academy of Sciences 101 (11), 3747-3752. arXiv:cond-mat/0311416
Brandes, U., 2001. A Faster Algorithm for Betweenness Centrality. Journal of Mathematical Sociology 25, 163-177.
Dijkstra, E. W., 1959. A note on two problems in connexion with graphs. Numerische Mathematik 1, 269-271.
Freeman, L. C., 1978. Centrality in social networks: Conceptual clarification. Social Networks 1, 215-239.
Freeman, L. C., Borgatti, S. P., White, D. R., 1991. Centrality in valued graphs: A measure of betweenness based on network flow. Social Networks 13 (2), 141-154.
Newman, M. E. J., 2001. Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Physical Review E 64, 016132.
Opsahl, T., Agneessens, F., Skvoretz, J. (2010). Node centrality in weighted networks: Generalizing degree and shortest paths. Social Networks 32, 245-251.
Tore Opsahl 
1.
Lauren Brent | December 7, 2011 at 10:44 pm
I’m finding your scripts very useful, in particular the randomisation functions. Any plans to expand your list of centrality measures? A weighted version of eigenvector centrality would be a great addition.
2.
Tore Opsahl | December 8, 2011 at 2:21 pm
Hi Lauren,
Thanks for your comment!
Indeed it would be great. If I do get time to program it, I will. Do you have any code for weighted eigenvector centrality?
Best,
Tore
3.
Till | February 22, 2012 at 8:45 am
The reference for (Barrat 2004) seems to be missing. I assume you mean this one:
A. Barrat and M. Barthelemy and R. Pastor-Satorras and A. Vespignani (2004). “The architecture of complex weighted networks”. Proceedings of the National Academy of Sciences 101 (11): 3747–3752.
4.
Tore Opsahl | February 22, 2012 at 7:11 pm
Thanks Till! There really should be a reference manager for WordPress! Tore
5.
Hamad Aljassmi | September 4, 2012 at 6:53 pm
Your site is full of great posts. I shall thank you that I learned a lot from your writings.
Is there any software around that could illustrate the degree strength (speed) data such as the A,B and C graphs shown in this post?
It seems that UcINET only provides a numerical label on the links that states the weights; please correct me if I am mistaken
6.
Tore Opsahl | September 4, 2012 at 7:04 pm
Hamad,
Thanks! You should be able to set the width of the lines in NetDraw (I believe I made these graphs in R). I would suggest you email them or their support email list.
Best,
Tore
7.
Ali | September 5, 2013 at 2:32 pm
Yet another thumbs up! I find your posts very useful, now that I seek to use Graph Theory for Text Mining. I am looking forward to completing these sections and to implementing some graphs using tnet in R.
8.
Yoma | January 2, 2015 at 10:40 am
Hi Tore
I have a doubt regarding the concept presented here. What is the advantage of considering number of ties separately (other than being closer to Freeman’s original idea)? Aren’t the other propositions (Barrat/Brandes) already implicitly (or indirectly) accounting for number of ties when they use SUM of weights?
Regards
Yoma
9.
Tore Opsahl | January 3, 2015 at 4:55 pm
Hi Yoma,
It depends on the outcome of your analysis. The second generation generalizations allow for a single number to describe the features. Even in a regression framework where multiple variables can be included, a single metric might be beneficial due to multicollinearity. If you look at the image of the three networks above, then you can see that the sum metrics does not discriminate among the three nodes yet they have a very different number of connections. Hence, the new metrics enable a more fine-grained analysis.
Tore
10.
kalmgren | April 10, 2015 at 12:32 am
Hey Tore,
I have read your paper many times, and I like your work. However, I have a question how did you prove your proposed centrality measure? Is it when you show the effect of tuning parameter?
One more question that is not related to your work, I understand what does the tuning parameter mean in your case. However, I don’t understand what tuning parameters are in general, can you please explain to me ?
Best regards,
Kyle
11.
Tore Opsahl | April 26, 2015 at 3:00 pm
Hey Kyle,
Let me start by the second questions: a tuning parameter is simply a number which is used to alter the metric to take different aspects into consideration.
The first question is a more difficult to answer. The metrics (I believe) are useful in that they (a) highlight a discrepancy in weighted node centrality metrics (i.e., they actually measure something else than the binary metrics they were based on), (b) provide a method for combining the existing binary and weighted metrics, and (c) provide reasonable results in empirical data. Nevertheless, it is always tricky to “prove” new metrics, and I don’t believe is simple formula for that exists.
Best,
Tore
12.
Saptarshi Mandal | January 24, 2016 at 2:24 am
How to deal with directed but asymmetric weighted networks in the tnet package
13.
Tore Opsahl | January 24, 2016 at 4:08 am
Hi Saptarshi,
tnet is written for directed networks with a weight attached to each tie. However, when analyzing undirected networks, two ties are formed between the nodes (one in each direction) with the same weight. Thus, it is straight forward to analyze undirected network with asymmetric tie weights as they are simply considered two directed ties.
Hope this answers your question,
Tore
14.
Saptarshi Mandal | January 24, 2016 at 8:03 am
Hi, Tore
I have provided a adjacency matrix as the input to the dichotomise_w function to obtain the network. But when i used this network to calculate the centrality measure i am getting this following error
Error in as.tnet(net, type = “weighted one-mode tnet”) :
There are duplicated entries in the edgelist
In addition: Warning message:
In Ops.factor(net[, “w”], 0) : ‘>’ not meaningful for factors
I am unable to resolve it. Please help.
15.
Tore Opsahl | January 26, 2016 at 12:22 am
Hi Saptarshi,
That error message is related to the existence of multiple ties between two nodes in the same direction. Please reach out by email (see the about page) with the code and data you are using.
Best,
Tore
16.
Atenea0208 | November 17, 2016 at 11:34 pm
Hi, Tore
I have the same error as Saptarshi, also can I send you my data ando code?
17.
Tore Opsahl | November 18, 2016 at 1:53 am
Sure. Tore
18.
Moritz | January 27, 2016 at 6:06 pm
Hi Tore,
I tried to calculate the betweenness centrality based on this edgelist: https://www.dropbox.com/s/c9e5gg35ie4yika/city_edgelist2.csv?dl=0
The graph is directed and weighted. The node with the ID “33” is one of the most central ones in the network. The formula betweenness_w provides values for some other nodes that which seem to be correct when looking at the visualization of the network. However no betweenness centrality for node “33” is given. I do not find an explanation for that. Do you have a solution for my problem?
19.
Tore Opsahl | January 29, 2016 at 5:32 am
Thank you for reaching out, Moritz.
Node 33 in your network only has outgoing ties, and no incoming ties. This means that it is never one a path between other nodes, and thus, its betweenness is 0.
Hope this helps,
Tore
# Load packages library("tnet") # Load datafile net <- read.table("city_edgelist2.csv", sep=";") # Degree k <- merge(degree_w(net, type="out"), degree_w(net, type="in"), by="node", suffixes=c(".out",".in")) # Show out-/in-degree of node 33 k[k[,"node"]==33,] # node degree.out output.out degree.in output.in # 33 22 41 0 020.
Moritz | April 29, 2016 at 12:24 pm
Thank you Tore for the fast response!
Another problem I am facing right now is the automatic exclusion of self-loops from the data after I loaded them.
Is there a way to switch off this step and allow self-loops to be considered in the calculation of betweenness centrality?
For most of the cases this does not make sense. But for my case it is quite important to incorporate these in the calculation of betweenness centrality. My network consists of corporate affiliates which are connected regarding their hierarchical position within the corporation to subordinate respectively superordinate corporate units. This is done for many corporations which are then aggregated on a city level (representing the nodes in the network). As major cities are defined by a 50km radius many ownership flows remain on a local scale (self-loops), thus controlling corporate affiliates at the outskirts of the city.
Thank you in advance for your help.
Best wishes,
Moritz
21.
Tore Opsahl | May 1, 2016 at 8:55 pm
Hi Moritz. I agree that it is important to adjust metrics to the data at hand. Since betweenness is defined as number of shortest path passing through a node, how would self-loops impact this metric? We can also continue this conversation by email if you’d like. Best, Tore
22.
Tae-jin | March 29, 2016 at 5:48 am
Hi Tore,
I appreciate all of your efforts.
I have a question how to calculate closeness and betewenness centraility measures for a directed weighted network by using tnet package. i.e. out_closeness_W and in_closeness_w / out_betewenness_w and in_betewenness_w.
Can I get these measures from tnet package?
23.
Tore Opsahl | March 31, 2016 at 11:48 pm
Hi Tae-Jin,
You can calculate the out and in-closeness / betweenness using the type parameter. See line 8 in the comment above.
Best,
Tore
24.
Ria | July 28, 2016 at 8:42 am
Hi, Mr. Tore,
Thank you for your great post.
I have a question, is this centrality measures also can be used for non integer weight, especially weight in range 0<weight<1?
Thank you.
Best regards,
Ria
25.
Tore Opsahl | July 28, 2016 at 12:54 pm
Hi Ria,
You can use non-integer weights with tnet.
Best,
Tore
26.
Ria | July 28, 2016 at 1:44 pm
Thank you for your fast response, Mr. Tore.
Based on your answer, then I can implemented this centrality measures for non-integer weighted network.
Since closeness value in tnet is closeness, not farness like in Ucinet. So my next question is, actor with good closeness measure is actor with big value for closeness?
27.
Tore Opsahl | August 12, 2016 at 2:32 pm
Hi Ria,
A higher closeness value represents a more central position in the network.
Best,
Tore
28.
Fen | August 10, 2016 at 4:45 am
Hi Tore,
Thanks for your great contribution. Your posts are very useful. I’m wondering if you have any updates including graph-level density, degree centralization for a directed and weighted network. Thank you very much.
Best,
Fen
29.
Tore Opsahl | August 12, 2016 at 2:40 pm
Hi Fen,
Glad you are finding the posts useful. tnet cannot compute graph-level density and degree centralization as these are not defined for weighted networks.
First, there has been many proposals for density in weighted networks. However, it is not clear what this is supposed to be as density is a metric between 0 and 1, and a maximum score is hard to define for weighted networks. For example, density could be defined as the sum of weights divided by (the number of ties times the maximum tie weight); however, this metric would become extremely sensitive to the maximum tie weight, and thus, a good metric for comparing networks (unless tie weights in all networks being compared were on a scale from, for example, 1 to 5).
Second, normalization of node centrality scores is, to my opinion, adding a bias to the data instead of removing one. In fact, I have stayed clear of standardising the measures due to what I believe was misleading in the original measures, let alone generalized ones. My main concern with the original ways of standardizing/normalizing node centrality measures (i.e., n-1) is that these scale linearly with the number of nodes. Specifically, I believe that none of the main three node centrality measures scales linearly. It has been argued that the average degree in networks does not change as a network grows. Hence, no scaling (i.e., use the average degree to compare networks). Also, closeness centrality is based on shortest distances. In small world networks, shortest distances does not scale linearly with the number of nodes, but rather logarithmically (i.e., divide farness scores by log(N) if your network is a “small world”). Finally, betweenness is based on n*(n-1) shortest paths, so it could be argued that it scales n-squared. Given these issues with the original measures, I have not given much thought/effort to normalize the generalized ones. Let me know if you figure out a way of doing it!
Best,
Tore
30.
Sylvert Tahalea | January 26, 2017 at 3:46 pm
Hi Tore,
Your contributions are great. I’m also study about centrality measure and other social network analysis method.
I’m wondering if you can help me about what the appropriate method for testing the centrality measure.
Thank you very much.
Best Regards,
Sylvert
31.
Tore Opsahl | January 27, 2017 at 12:14 am
Hi Sylvert,
The appropriate method for defining centrality depends on the research context. I would suggest Freeman’s article from 1978/9 to learn more.
Best,
Tore
32.
zhaiyanqi | February 23, 2017 at 2:38 pm
Hi Tore,Your contributions are great.I am using your method .But I have a question.When you calculate the betweeness centrality above ,you have just got the number of the shortest paths through the node,but you have not dived by the total number of the shortest paths,As you have said in the paper!
33.
Tore Opsahl | February 23, 2017 at 5:49 pm
Hi Zhaiyanqi,
The above example does not not multiple shortest paths between nodes. As such, the counts are all divided by 1.
Hope this helps,
Tore
34.
zhaiyanqi | February 24, 2017 at 8:23 am
Thank you for your reply, so In the actual evaluation work when i use the R program，and I get the number of the shortest paths through the node i is n ,In fact n/1 is the score of the node i. Is it your method you have metion above”the counts are all divided by 1″?why you use n/1? if is better to multiple shortest paths between nodes and then sum ?
The second question: if i want to get only one closeness score of the node i in the weight collaboraton network or weight citation network which is alpha value is better 0.5 or 1 or 1.5 ,and could you explain the actual meaning of different alpha value in the two different network? I am a little confused.
Thank you very much.
Best Regards,
Yanqi Zhai
35.
Tore Opsahl | February 25, 2017 at 12:48 am
Glad you are using tnet. The function gives you the number of shortest paths that pass through a node (see example).
The alpha value determines the weight attached to tie weights. Please see the paper for an in-depth discussion of the alpha parameter.
Good luck!
Tore
36.
zhaiyanqi | February 24, 2017 at 1:42 pm
Hi Tore,i come up another question, when i use your method to calculate the degree centrality.
degree_w(dected.net, measure=c(“degree”, “input”, “alpha”), alpha=0) how can i calculate the indegree of the node, the program is right?
the second question : when you calculate the degree centrality do you consider the method to normalize the degree and the weight
before combine them together using alpha?
Best Tore
37.
Tore Opsahl | February 25, 2017 at 12:50 am
Hi Yanqi,
To get the in-degree, you can set the type parameter to in. For example: degree_w(dected.net, measure=c(“degree”, “input”, “alpha”), alpha=0, type=”in”). For more details, see the help file: ?degree_w
The alpha metric is computed without normalization.
Best,
Tore
38.
zhaizhai | February 24, 2017 at 2:37 pm
1 2 2
1 3 2
2 1 4
2 3 4
2 4 1
2 5 2
3 1 2
3 2 4
5 2 2
5 6 1
when i use the R program to calculate the closeness centrality of the above directed network
.closeness_w(dected.net, alpha=0) //the R program
is it right to write it ? Is it the same program with the undirected network?When alpha =1,before calculate the shortest distance do you also multiple the average weight to normalize?because i find you multiple the average weight in the undirected network. However, in the directed network,how to calculate the average weight or how to normalize, in fact there are two directions.
Thank you very much !
39.
Tore Opsahl | February 25, 2017 at 12:52 am
Hi,
I am not entirely sure what you mean. Please reach out be email and I will get back to you.
Best,
Tore
40.
zhaizhai | February 25, 2017 at 8:52 am
Thank you Tore! I am appreciate!I will send to your email later!
zhaizhai
41.
Rachel McGihon | March 15, 2017 at 3:13 pm
Hi Tore,
Thank you for your posts, they have been very helpful!
I am having some difficulty interpreting output for betweenness centrality and was hoping that you could provide some clarification. I have obtained the following R output:
> betweenness_w(net1, directed = TRUE, alpha = 1)
node betweenness
[1,] 1 0.3333333
[2,] 2 2.3333333
[3,] 3 1.0000000
[4,] 4 0.0000000
[5,] 5 0.0000000
[6,] 6 0.0000000
[7,] 7 1.0000000
[8,] 8 0.0000000
I was under the impression that the betweenness centrality reflects the number of shortest paths that pass through a node. If this is correct, how is it possible to have non-integer values? How would you interpret these?
Thank you in advance for your help.
Rachel
42.
Tore Opsahl | March 16, 2017 at 12:31 am
Glad the posts have been helpful, Rachel.
Between is the number of shortest path between two nodes that pass through the focal node. However, if there are two or more paths between two nodes that (a) have the same length and (b) this length is the shortest, then the count for the nodes on those paths are incremented by 1/the number of shortest paths. For example, let’s say that there are two shortest paths between nodes A and B: one through node C and one through node D, then a score of 1/2 is added to both node C and node D.
Hope this helps,
Tore
43.
Justyna | May 9, 2017 at 5:08 pm
Hi Tore,
I was wondering if there is a way of explaining how adding/removing nodes to the network affect the closeness centrality calculated in the way you propose (or in any other way for that matter). I’ll try to make clear what I mean by that by analogy with degree. If I add one edge to a network, I know it will affect (increase by one) the degree of the two nodes it connects and that no other node is affected. Now, closeness is a measure that takes into account the entire network. Is there a way of explaining how adding a node (or a fixed number of nodes) will affect a closeness of any given node? I realize that it cant be answered precisely, as the calculation will vary significantly from one network to another. But is there a general sense for how it should affect the measure?
Let me know if my question is not clear and I’ll try to be more specific.
Justyna
44.
Tore Opsahl | May 9, 2017 at 9:50 pm
Hi Justyna,
This is a hard question as closeness depends more on the ties that the nodes bring with them to the network. If a node that bridges two disconnected components, a large change can occur to the closeness metrics. Conversely, adding isolates or nodes outsides the main component will not change the closeness metric.
Best,
Tore
45.
Tobi | June 2, 2017 at 6:56 am
Hi Tore!
I have a problem with calculating the weighted betweennes for my network and don’t understand why my output looks the way it looks. I have a complete network with 79 nodes and weighted edges with levels ranging from 0.091 to 362’923. Since it is a complete network the alpha parameter can be set to one in order to neglect the effect of multiple edges on the betweennes score (is this correct or am I wrong?). With the code betweenness_w(“network name”,directed=TRUE,alpha=1) I get the following output:
[1,] 1 0
[2,] 2 0
[3,] 3 0
[4,] 4 0
[5,] 5 0
[6,] 6 0
[7,] 7 0
[8,] 8 152
[9,] 9 0
[10,] 10 0
……
There are many zeros. Is this because of the very big difference in levels of the edges or is this related to the completeness of the network?
Thank you very much for your efforts!
best,
Tobi
46.
Tore Opsahl | June 2, 2017 at 7:08 pm
Hi Tobi,
The distribution of betweenness scores is often zero inflated. If there are central nodes with strong ties, they become key intermediaries among others.
If you have any questions, email me a copy of the data and the code. I will quickly check it.
Best,
Tore
47.
Helen | July 14, 2017 at 5:41 pm
Hello Tore
Thanks for much for the informative blog. I was hoping you could help me with a quick question, when you are calculating closeness (in igraph) on a weighted (and directed) network, what value is returned for nodes that are not connected (equivalent to the sum of all nodes being returned in an unweighted network) or are weights rescaled such that the total number of nodes is still used?
Many thanks. Helen
48.
Tore Opsahl | July 17, 2017 at 1:56 am
Hi Helen,
I am not entirely sure about igraph — you would have to contact the guys behind it. However, I know that igraph considers a lower tie value to be stronger (tnet considers a higher tie value to be stronger). For disconnected network, I am not sure how igraph deals with it. In tnet, you can set the gconly to be FALSE to get the closeness score of disconnected nodes. See https://toreopsahl.com/2010/03/20/closeness-centrality-in-networks-with-disconnected-components/
Best,
Tore
49.
Kamil | September 18, 2017 at 8:41 am
Hi Tore,
I am new to the centrality measures and this post is very informative, it helped me understand in the first place. I was hoping you could help me with a problem. My work mostly focus on betweenness. I was wondering if there is a faster algorithm to calculate betweenness in weighted graphs with small number of KNOWN weights. For instance, weights of edges in my system are restricted with {1,2,3,4}. I want to calculate betweenness of each node. But there are a lot of nodes and Running time of Dijkstra’s algorithm looks unfair to me against unrestricted weighted graph. If you know a way, could you help me?
Thanks,
Kamil
50.
Tore Opsahl | September 19, 2017 at 2:56 am
Hi Kamil,
I am sure there are more efficient ways of computing betweenness. I have focused more on producing a number that easily matches intuition (e.g., inverting tie weights). If you come up with a faster method, I am happy to update the way tnet computes betweenness.
Best,
Tore
51.
Aldo Ivan Parra | November 17, 2017 at 8:35 pm
Hi Tore,
Your contribution here is superb, congrats. I want to ask you about the tie weights considered as costs. what happen if the weights represent capacity or speed? I want to privilege the paths that have higher tie weights (high farness isn´t?) If I run closenness_w do I need to check the lower values to find who is central?
52.
Tore Opsahl | November 18, 2017 at 2:26 pm
Hi Aldo,
The closeness function (and more generally, the shortest path function) inverts tie weights so that a higher value means higher capacity. Normally in shortest path algorithms, tie weights represent cost or distance. Have a look at this page: https://toreopsahl.com/tnet/weighted-networks/shortest-paths/
Best,
Tore
53.
Aleksandre Gogaladze | February 7, 2018 at 10:29 am
Dear Tore,
Thank you very much for all this valuable information. I am a biologist by training and SNA is a new field for me so just now I am in a process of finding out about all the network-wide and node specific statistical parameters. I have encountered a problem reproducing weighted closeness centrality values myself using the formula you provide in your article (Opsahl et al. 2010). E.g. if we have a very simple 3 node weighted directed graph:
linkstest <- cbind(
i=c(1,1,2,2,3,3),
j=c(2,3,1,3,1,2),
w=c(1,2,4,4,1,2))
closeness_w(linkstest, directed = T, alpha=1)
node closeness n.closeness
[1,] 1 0.2857143 0.1428571
[2,] 2 0.8571429 0.4285714
[3,] 3 0.3428571 0.1714286
Now using the formula if I want to calculate closeness e.g. for node 1, I get the weighted distance of 1/3+1/5 = 0.53 and to the power of -1 = 1.87 and I cannot understand how r calculates 0.28 for the node 1.
Could you please help me understanding the mathematics behind? am I missing something from the formula?
Thanks a lot for your help in advance.
Best regards,
Aleksandre
54.
Tore Opsahl | February 13, 2018 at 1:57 am
Hi Aleksandre,
The best way to understand the code is often to look at the implementation. I chose to write all of tnet using R code and rely on other packages for the heavier computation to increase transparency. For example, by typing closeness_w without () at the end, the underlying code will be displayed.
In your example, I have computed the distance matrix along with the row sum and inverse row sum below. Hope this explains it.
Good luck,
Tore
X1 X2 X3 rowSums invRowSums 1 NA 2.333333 1.1666667 3.500000 0.2857143 2 0.5833333 NA 0.5833333 1.166667 0.8571429 3 1.7500000 1.166667 NA 2.916667 0.342857155.
Aleksandre Gogaladze | April 13, 2018 at 11:46 am
Hi Tore,
Thanks a lot. Now I understand it. your comment was very helpful.
Best regards,
Aleksandre
56.
Ana | July 26, 2018 at 3:38 pm
Hi Tore! Great contribution this page, the R package and articles!!
I have two problems.
1) I am trying to estimate betweenness_w in a directed and weighted graph. However, when I change alpha to 0 or 1 the results is the same. For example:
## This is the net:
m.tnet
i j w
1 2 2
1 3 4
2 4 2
2 5 1
3 6 2
3 7 1
4 8 3
4 9 4
5 10 3
5 11 4
## Result 1:
betweenness_w(m.tnet,alpha=0)
node betweenness
[1,] 1 0
[2,] 2 6
[3,] 3 2
[4,] 4 4
[5,] 5 4
[6,] 6 0
[7,] 7 0
[8,] 8 0
[9,] 9 0
[10,] 10 0
[11,] 11 0
## Result 2:
betweenness_w(m.tnet,alpha=1)
node betweenness
[1,] 1 0
[2,] 2 6
[3,] 3 2
[4,] 4 4
[5,] 5 4
[6,] 6 0
[7,] 7 0
[8,] 8 0
[9,] 9 0
[10,] 10 0
[11,] 11 0
## Result 3:
betweenness_w(m.tnet,alpha=0.5)
node betweenness
[1,] 1 0
[2,] 2 6
[3,] 3 2
[4,] 4 4
[5,] 5 4
[6,] 6 0
[7,] 7 0
[8,] 8 0
[9,] 9 0
[10,] 10 0
[11,] 11 0
It is always the same! Could you help me?
Thanks,
Ana
57.
Tore Opsahl | July 26, 2018 at 9:43 pm
Hi Ana,
The network is very simply and contain few triads (e.g., 2->5->11) which would increase the intermediary node’s score by 1. The alpha parameter simply changes which paths are taken. Please see the paper.
Good luck with your work.
Tore
58.
Ana | July 27, 2018 at 8:19 am
Thanks Tore!
But look at the nodes 4 and 5. Both participate in 4 shortest path:
4 in 1->2->4->8; 2->4->8; 1->2->4->9; 2->4->9
5 in 1->2->5->10; 2->5->10; 1->2->5->11; 2->5->11
When weights are not considered both have betweenness = 4.
However, when weights are considered (alpha >0) I will expect that node 4 would have higher betweenness than node 5, since node 4 has more weight in one path. So I think, I am not understanding how the weights are playing!
Thanks!
Ana
59.
Tore Opsahl | August 1, 2018 at 11:11 pm
HI Ana,
The alpha simply controls the paths being chosen as the shortest. It does not increase the betweenness score. Betweenness is defined as the count of paths that go through a node. This is in contrast to closeness where the metric is the sum of inverse weights.
Best,
Tore
60.
Ana | August 2, 2018 at 8:32 am
Thanks for the replay!
I that case, I don’t understand how alpha could control the paths being chosen as the shortest, since the shortest path is only one in a network.
Thanks again!
Ana
61.
Tore Opsahl | August 3, 2018 at 5:44 pm
Hi Ana. Your network is a tree, and as such, there aren’t multiple paths between nodes. The weighted versions of betweenness requires this to produce a different result than the binary one. Have a look at the figure with three paths between nodes A and B (Figure 3 in the paper).
Best,
Tore
62.
Ana | August 6, 2018 at 8:09 am
Thanks! Tore!
63.
Luke | August 23, 2018 at 4:59 pm
Hey Tore-
Thanks so much for this. I’m trying to understand how calculating the betweenness for a node works in a weighted graph where we only care about edge weights (i.e. alpha = 1). Where does the distance between two nodes come into play, especially if you have one shortest path between two nodes and that path goes through the node you’re measuring betweenness for. Doesn’t the exponential approach still just leave you with a betweenness of 1? I feel like I’m missing something.
Thanks!
Luke
64.
Tore Opsahl | August 26, 2018 at 8:44 pm
Hi Luke,
The tie weights come into consideration when identifying the shortest path. In a weighted network, this is the path with the smallest sum of tie weights between two nodes. When computing betweenness, all the nodes on the path between the two nodes with the smallest sum of tie weights gets 1 added to their betweenness score.
Good luck!
Tore
65.
Yingjie | October 23, 2018 at 4:30 am
Hi Tore,
Great work. Thanks for your contributions! I got the following error message when computing centrality scores (degree and closeness) and would very much appreciate any ideas on how to solve it:
Error in as.tnet(net, type = “weighted one-mode tnet”):
There are duplicated entries in the edgelist
This error occurred to all team networks with missing edge values (in these cases one or two nodes did not respond). And there are no multiple ties between nodes.
I feel it might have something to do with missing edge values. But do you have an answer to this?
Thanks a lot!
Yingjie
66.
Tore Opsahl | October 24, 2018 at 10:19 am
Hi Yingjie,
tnet is not able to handle missing values in the edgelist. I don’t know if a good way of dealing with missing data when computing network metrics. If you remove these, do you get the same error message?
Best,
Tore
67.
Hyemin Chung | February 11, 2019 at 6:36 am
Hi, Tore, Thank you for your great work and contribution.
I have a question for the Betweenness centrality. You counted only ‘ the number of shortest paths that pass through a certain node ‘, unlike what you proposed in your paper. Is there any special reason that you didn’t make the tnet function in this way? Why didn’t you divide it by the total number of the shortest path? If the it is divided, this weighted betweenness centrality would also mean the rate of the shortest path that pass the certain node among the whole shortest path, just like the Freeman’s one.
What I am trying to do through tnet is to compare the results measured by freeman’s BC and your BC, to see how the network analysis result varies when reflecting edge weights.
I would really love to hear your answer.
Best,
Hyemin
68.
Tore Opsahl | February 25, 2019 at 8:59 pm
Hi Hyemin,
The method does divide the count by the number of shortest paths.
Best,
Tore
69.
Melissa | October 30, 2020 at 2:27 pm
Hello Tore,
First – thank you for all of your work!
Second – I have a question about tnet’s betweenness_w/alpha value, and how to choose an appropriate ‘standard’ tie weight against which to normalise other tie weights. I am part of a research project which uses network analysis – but we are not mathematicians and wanted to ask the expert!
Our method is as follows.
We take a template ‘baseline’ network with all tie weights of the same value (usually weight = 1), and apply betweenness_w with alpha = 0.5. Then we *decrease* some tie weights (for example, Tie X and Tie Y now have weight = 0.5), and reapply betweenness_w with alpha = 0.5, to compare centrality results for this adjusted network against the baseline network results. The idea is to see which nodes have experienced the most change, and discuss these.
What we’d like to do now is simultaneously *increase* some tie weights and *decrease* other tie weights, in comparison to the baseline, and run betweenness_w with alpha = 0.5 again. For example, where all baseline tie weights = 1, Tie X has lost 50% of its original functional capacity so has weight = 0.5 and Tie Y has gained 50% of its original functional capacity so has weight = 1.5.
We have run a few tests to determine if:
(1) some baseline tie weight values are more sensitive than others (if the baseline tie weights are all 0.25, or all 0.5, or all 1, etc., does this have implications for betweenness_w with alpha = 0.5)? Centrality results appear the same regardless of the standard tie weight value we choose *as long all ties are of equal weight*.
(2) decreasing tie weights or increasing tie weights has proportionally the same effect on centrality results. For example, for a network where the baseline standard tie weights all = 1, are the centrality results more or less affected if you decrease the weights of Tie X and Tie Y to 0.5, vs. if you increase the weights of Tie X and Tie Y to 1.5? It seems that decreasing tie weights has *less* impact on centrality results (compared to the baseline results) vs. increasing tie weights (compared to the baseline results). In other words, centrality results are more sensitive to an increase in tie weight than a decrease in tie weight. We think this is because the alpha tuning parameter transforms the ‘input’ weight to an inverse ‘output’ weight compatible with igraph calculations, in a non-linear manner:
– ‘input’ weight of 0.25 transforms to an ‘output’ weight for igraph of 2.00
– ‘input’ weight of 0.50 transforms to an ‘output’ weight for igraph of ~1.41
– ‘input’ weight of 0.75 transforms to an ‘output’ weight for igraph of ~1.15
– ‘input’ weight of 1.00 transforms to an ‘output’ weight for igraph of 1.00
– ‘input’ weight of 1.25 transforms to an ‘output’ weight for igraph of ~0.89
– ‘input’ weight of 1.50 transforms to an ‘output’ weight for igraph of ~0.82, etc.
(3) point 2 interacts with point 1. Given the nonlinear output weights in point 2, it appears so. In other words if in the baseline all tie weights = 0.5, and in the adjusted network a handful of increased tie weights = 0.75, does that affect centrality results to a greater extent than if the baseline tie weights = 1 and that same handful of increased tie weights = 1.5? It seems the lower you set the baseline tie weight value (e.g. all tie weights = 0.25), the less linear or ‘proportionate’ the impact of decreasing vs. increasing a tie’s weight.
All of this is to ask: what would you recommend as a ‘standard’ or baseline tie weight value, if we want to reflect the impact of a tie weight decrease and the impact of a tie weight increase in a more proportional way?
Or perhaps this could be done by fitting a linear function for alpha? Are we missing something essential about network science here (very possible!)? Maybe this apparent ‘sensitivity’ is due to the size and structure of our particular network (a five-level hierarchy of ~480 nodes and ~4200 ties)?
Thank you for your help!
Best wishes,
Melissa
70.
Arlo | April 5, 2021 at 10:58 pm
Hi Tore,
Thanks for your wonderful work! I am currently working on a weighted and un-directed network. I try to get degree centrality with different alpha values. However, I notice for different alpha, the resulting degree centrality sequence does not change for my data. I wonder is it normal (That is, degree centrality stays regardless the change of alpha). Thanks!
71.
Connor | July 8, 2021 at 9:53 am
Hi Arlo,
I am having this same issue as well and would love to hear if you figured out what was going on with your data! I am also using a weighted/un-directed network with parallel edges converted to weights. I typically work with matrices so I’m wondering if there is an error when I convert my data to an edgelist.
72.
Connor | July 8, 2021 at 9:58 am
I just read through previous comments and found out my answer! (Sorry for multiple replies). Thank you again for all your help with this Tore!